Medelv.:

Stand.:

Min:

Max:

Visa en fördelning per maskin

Visa gemensam fördelning

Antal mätvärden per maskin:

Totalmedelvärde:

Medelavvikelse maskin 1:

Medelavvikelse maskin 2:

Medelavvikelse maskin 3:

Medelavvikelse plasttyp 11:

Medelavvikelse plasttyp 12:

Standardavvikelse (maskin 1-3):

Undre toleransgräns:

Övre toleransgräns:

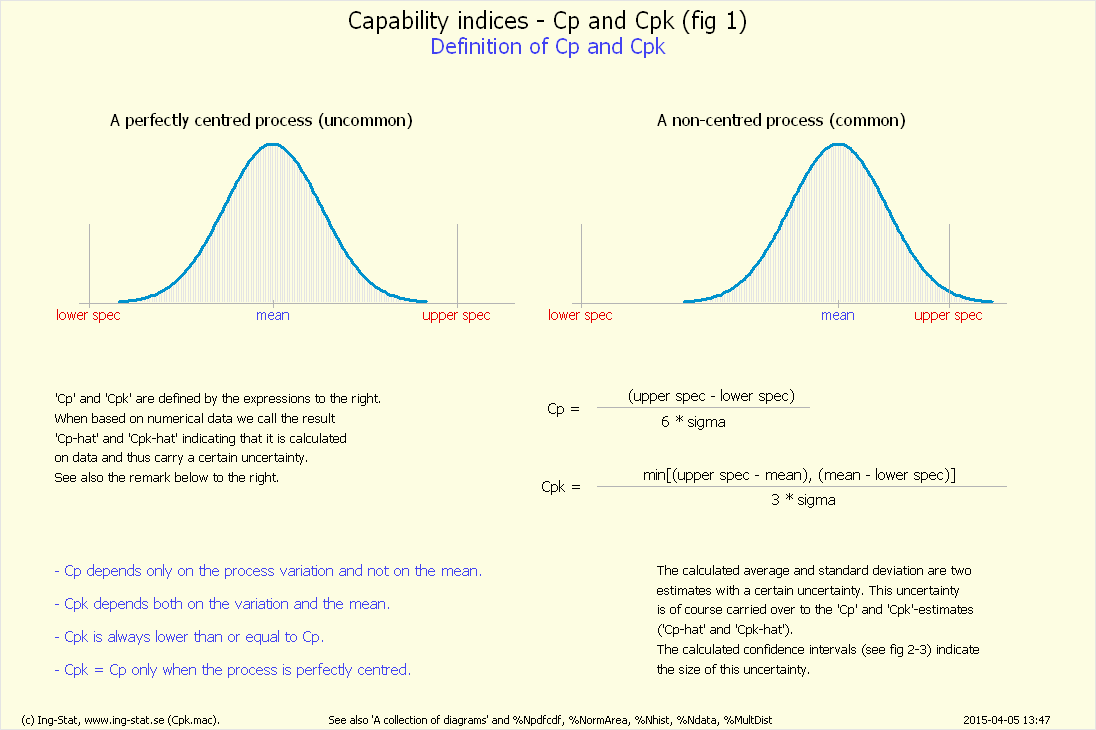
%Cpk (fig 1)...

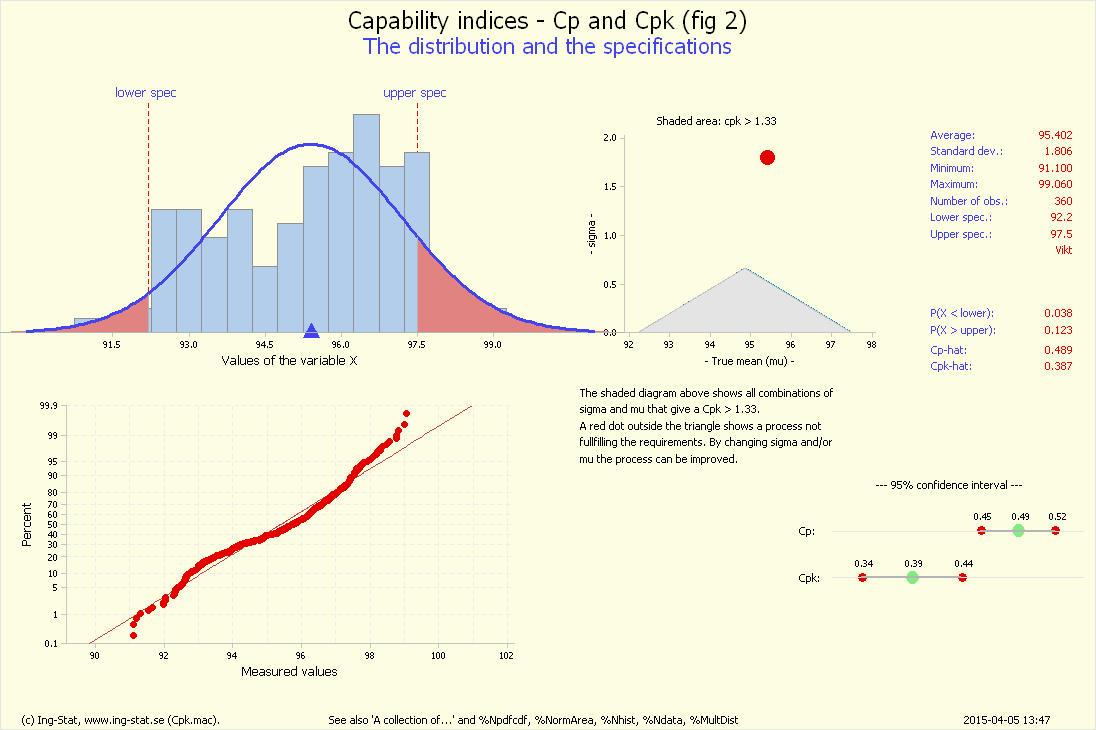
%Cpk (fig 2)...

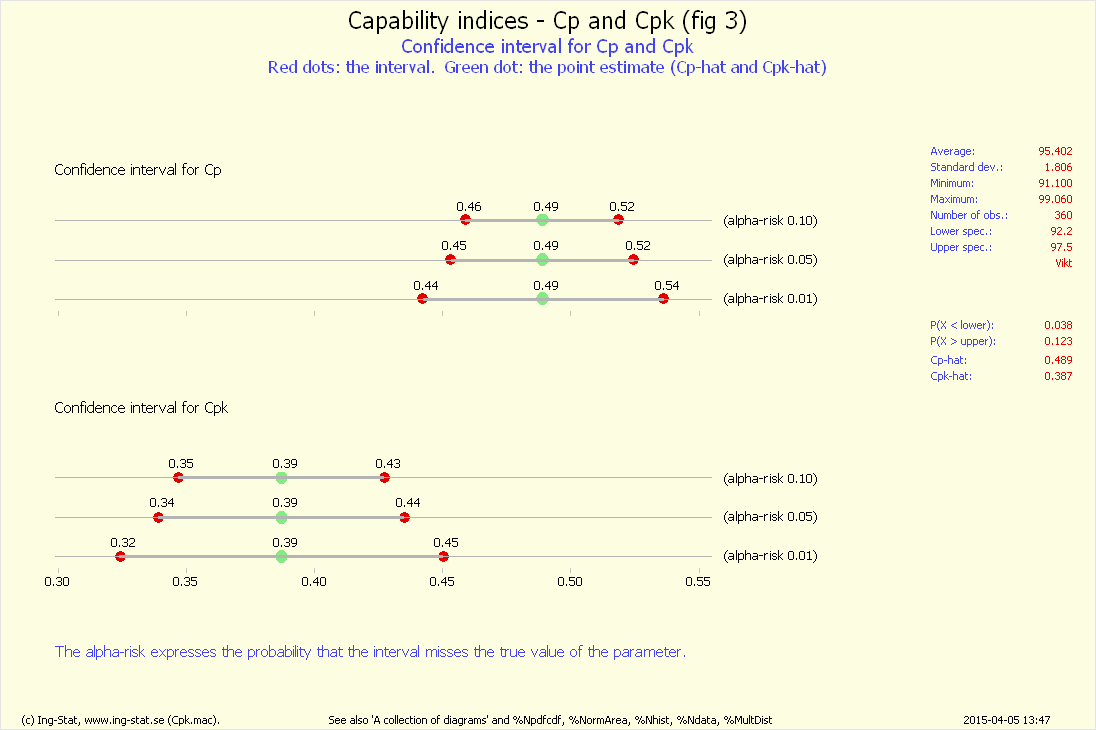
%Cpk (fig 3)...

Rutan visar tre fördelningar: blå är 'maskin 1', röd är 'maskin 2' och grön är 'maskin 3'. (Om det syns bara en eller två fördelningar innebär det att två eller fler maskiner har samma medelavvikelse.)
De tre vertikal linjerna motsvarar de två specifikationsgränserna (röda) samt processens medelvärde (grå).
Varje fördelning är en blandning av två plasttyper och om dessa har tillräckligt olika medelavvikelser, blir fördelningarna icke-symmetriska eller – om medelskillnaden är ännu större – tvåtoppiga.

Om markören förs över graffönstret visas en vertikal blå linje. Det ena värdet är linjens läge på X-axeln, det andra värdet är avståndet i procent till de två toleransgränserna. Klicka på den blå linjen för att lagra ett nytt totalmedelvärde för processen.

Med de två radioknapparna ovan fördelningarna är det möjligt att visa den totala fördelningen. Denna motsvarar det histogram som visas i Minitab då nedanstående kommandon har körts.

Observera 1/3 av alla mätningar gäller 'plasttyp 11' och 2/3 gäller 'plasttyp 12' (detta är inprogrammerat). De två plasttyperna är slumpmässigt fördelade över de tre maskinerna.

••••

'Kopiera/Klistra in' raderna i rutan nedan till 'Session window' i Minitab vid "MTB >"-prompten och tryck sedan på [Enter]-knappen på tangentbordet.

Första två raderna simulerar data för den angivna övningen. Övriga rader är förslag på analys och grafer.

Om värdet ändras i någon av indatarutorna visas ett antal radioknappar som skriver in motsvarande kommandon i rutan.

••••

De tre sifferuppgifterna visar det teoretiska medelvärdet och den teoretiska standardavvikelsen (sigma) samt 'Cpk'-värdet på det resultat som når kunden då processen har nuvarande prestanda.
När t.ex. skillnader mellan maskiner och skillnad mellan plastmaterial minskas, minskar också spridningen (sigma) och 'Cpk'-värdet ökar på resultat som når kunden.

Indatarutan 'Standardavvikelse:' är spridningen som åtstadkoms av andra variationskällor (dvs inte den variation som kommer av skillnader mellan maskiner eller plastmaterial).

Klicka på radioknappen "Visa gemensam fördelning" (över grafen) för att se fördelningen av resultat som når kunden. (Alla uppgifter kan jämföras med grafen 'fig 2' som skapas efter Minitab-körningen.)

••••

Övning 1 – en första körning
Överför kommandona till Minitab-fönstret och tryck [Enter]. Grafen märkt 'fig 2' sammanfattar mätningarna. Totalmedelvärdet är ungefär 95.4 och standardavvikelsen är ungefär 1.8, Cpk är ungefär 0.39. Processen är alltså inte duglig enligt vanlig standard. Kör 'övning 2'.

Övning 2 – ingen skillnad mellan maskiner
I denna körning finns det ingen skillnad mellan maskinerna. I 'fig 2' visas att medelvärdet är fortfarande ungefär 95.4 och standardavvikelsen har minskat till ungefär 1.0 och Cpk har ökat till ungefär 0.74. Processen är fortfarande inte duglig. Kör 'övning 3'.

Övning 3 – ingen skillnad mellan plaster
I denna körning finns det heller ingen skillnad mellan plaster. I 'fig 2' visas att medelvärdet är fortfarande ungefär 95.4 och standardavvikelsen har minskat till ungefär 0.9 och Cpk har ökat till ungefär 0.78. Processen är fortfarande inte duglig. Kör 'övning 4'.

Övning 4 – förändring av medelvärde, standardavvikelse eller specifikationer
Denna körning utgår ifrån 'övning 3'. Gör en körning i Minitab och avgör i 'fig 2' hur man kan förändra medelvärde eller standardavvikelse eller processens specifikation så att processen får ett Cpk > 1.33. ändra sedan i rutorna och gör en ny körning. Det kan behövas flera körningar. (Tips: högerklicka triangeln och använd 'Crosshairs' för lättare att avgöra var den röda punkten ligger.)

Övning 5 – 'probability plots' över maskiner
I denna övning finns det bara skillnader mellan maskinerna, ingen materialskillnad. En 'probability plot' visar tre parallella linjer, något förskjutna. Det betyder att de tre maskinerna har ungefär samma standardavvikelse (spridning) men olika medelvärden. Resultatet ges också som siffror i en tabell.

Övning 6 – histogram över maskiner
I denna övning finns det bara skillnader mellan maskinerna, ingen materialskillnad. En graf visar tre histogram, något förskjutna. Resultatet ges också som siffror i en tabell.

Övning 7 – ett matrisdiagram
I denna övning ritas ett s.k. matrisdiagram över data. Då man har många kolumner ger ett matrisdiagram en snabb överblick. Analysen underlättas om man använder s.k. 'brushing' (högerklicka diagrammet).

Övning 8 – ingen skillnad mellan maskiner, minskad spridning
Ändra manuellt i rutorna så att alla avvikelser för maskin 1, 2 och 3 blir 0. Minska standardavvikelsen till 0.6. Notera att fördelningen passar ganska väl inom toleransgränserna men att den systematiska skillnaden mellan plastmaterialen framträder. Det finns alltså utrymme för ytterligare kvalitetsförbättringar genom att undersöka och eliminera skillnader mellan materialen.

Övning 9 – ingen skillnad mellan maskiner eller material, Cp = Cpk = 1
Ändra manuellt i rutorna så att alla avvikelser för maskiner och plasttyper blir 0. Skapa en centrerad process och välj en standardavvikelse så att det blir exakt 6 standardavvikelser mellan undre och övre specifikationsgräns. Notera att fördelningen passar precis inom specifikationsgränserna. Kör %Cpk i Minitab och notera att Cp och Cpk blir nära 1.

Övning 10 – ingen skillnad mellan maskiner eller material, Cp = Cpk = 1.33
Ändra manuellt i rutorna så att alla avvikelser för maskiner och plasttyper blir 0. Skapa en centrerad process och välj en standardavvikelse så att det blir exakt 8 standardavvikelser mellan undre och övre specifikationsgräns. Notera att fördelningen passar väl inom specifikationsgränserna. Kör %Cpk i Minitab och notera att Cp och Cpk blir nära 1.33.

••••