t-test - utbildningsdata

dataA     <- rnorm(antalA, myA, sigmaA)                      # Skapar data A.
dataB     <- rnorm(antalB, myB, sigmaB)                      # Skapar data B.
konflevel <- konf                                            # Konfidensnivå

t.test(dataA, dataB, alternative = 'two.sided',              # Kommando för t-test.
   mu = 0, paired = parad, var.equal = varians,                 
   conf.level = konflevel)

#------------------------------- Nedan skapas två grafer (dataA och DataB)

library(ggplot2)

list1 <- rep(c("A"), each=antalA)
list2 <- rep(c("B"), each=antalB)
Mangd <- c(list1, list2)

minaData <- data.frame(c(dataA, dataB))
minaData <- data.frame(minaData, Mangd)

colnames(minaData)[1] <- "Mätresultat"
colnames(minaData)[2] <- "Maskin"

medelA <- mean(dataA)
medelB <- mean(dataB)

stdA  <- sd(dataA)
stdB  <- sd(dataB)

a <- medelA - 3.1*stdA
b <- medelB - 3.1*stdB
d <- medelA + 3.1*stdA
e <- medelB + 3.1*stdB

xmin <- min(a, d, b, e)
xmax <- max(a, d, b, e)

# ---------------------------------------------- Nedan: histogram ----------------

ggplot(minaData, aes(Mätresultat)) + geom_histogram(bins=15, color='black', alpha = 0.5, aes(y = after_stat(density), fill = Maskin), position = 'identity') + 
    labs(x = "Simulerade värden", y = "") + 
    theme(axis.title.x = element_text(size = 16), axis.text.x = element_text(face = "bold", color = "black", size = "14")) + theme( axis.text.y = element_blank()) +
    stat_function(fun=dnorm, color='red',  linewidth=1.0, args=list(medelA, stdA), xlim = c(a, d)) +
    stat_function(fun=dnorm, color='blue', linewidth=1.0, args=list(medelB, stdB), xlim = c(b, e)) +
    coord_cartesian(xlim = c(xmin, xmax))
   
    
# ---------------------------------------------- Nedan: normalfördelningsdiagram ----------------
    
ggplot() + coord_flip() + labs(y = "Simulerade värden", x = "") + theme(axis.title.x = element_text(size = 16), axis.text.x = element_text(face = "bold", color = "black", size = "14")) + theme( axis.text.y = element_blank()) + 
stat_qq(aes(sample = dataA), colour = "red") + 
stat_qq(aes(sample = dataB), colour = "blue") +
stat_qq_line(aes(sample = dataA), colour = "red") + 
stat_qq_line(aes(sample = dataB), colour = "blue")

# ----------------------------- Nedan: histogram (skillnaden dataA - DataB) ----------------

skillnadAB = dataA - dataB

minaData <- data.frame(skillnadAB)

colnames(minaData)[1] <- "Skillnad"

medelAB <- mean(skillnadAB)
stdAB   <- sd(skillnadAB)

xmin <- medelAB - 3.1*stdAB
xmax <- medelAB + 3.1*stdAB

skillnadHistogram <- ggplot(minaData, aes(x=Skillnad))
skillnadHistogram <- skillnadHistogram + geom_histogram(binwidth=0.5, colour='black', fill='yellow', aes(y = after_stat(density)))
skillnadHistogram <- skillnadHistogram + stat_function(fun=dnorm, color='red', args=list(medelAB, sd=stdAB))
skillnadHistogram <- skillnadHistogram + xlim(xmin, xmax)
skillnadHistogram

# --------------------- Nedan: normalfördelningsdiagram (skillnaden dataA - DataB) ---------
    
ggplot() + coord_flip() + labs(y = "Skillnader A B", x = "") + theme(axis.title.x = element_text(size = 16), axis.text.x = element_text(face = "bold", color = "black", size = "14")) + theme( axis.text.y = element_blank()) + 
stat_qq(aes(sample = skillnadAB), colour = "red") + 
stat_qq_line(aes(sample = skillnadAB), colour = "red")

Utgångsläge Övning 1

Medelv.:

Stand.:

Min:

Max:

Info, referenser, m.m...

Visa en fördelning per process

Visa gemensam fördelning

Visa/dölj programkod för R

Visa/dölj kommentarer

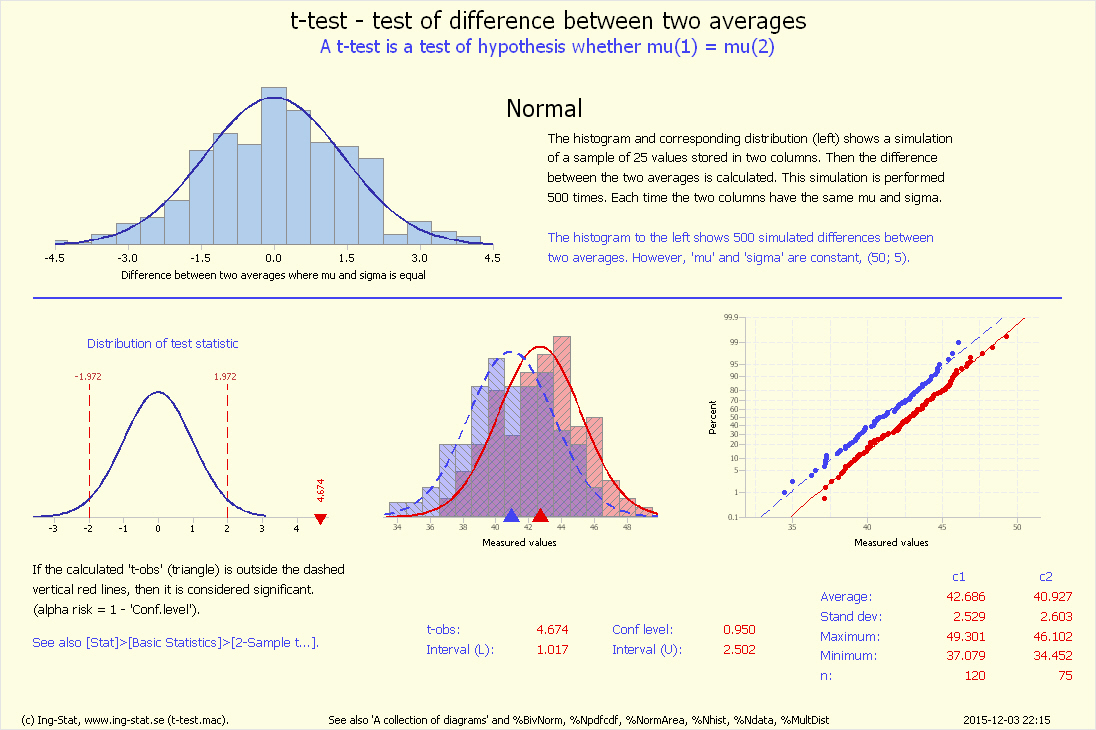
5. t-test – en jämförelse mellan medelvärden

"Är μ_A = μ_B eller μ_A ≠ μ_B"

Antal mätvärden process A:

Medelvärde process A:

Standardavvikelse process A:

Antal mätvärden process B:

Medelvärde process B:

Standardavvikelse process B:

Konfidensnivå (0.50 - 0.99):

Sigma antas lika i A och B

'Paired t-test'

En artikel

Antal mätvärden process A: Här anges antal mätvärden från process A.

Medelvärde process A: Här anges medelvärdet för process A.

Standardavvikelse process A: Här anges standardavvikelsen för process A.

Antal mätvärden process B: Här anges antal mätvärden från process B.

Medelvärde process B: Här anges medelvärdet för process B.

Standardavvikelse process B: Här anges standardavvikelsen för process B.

Konfidensnivå: Alla statistiska test har en sannolikhet (risk) att felaktigt ge 'signifikant resultat' dvs slumpmässig variation ger analysen ett felaktigt svar. Denna risk är (1 - konfidensnivå).

Sigma antas lika i A och B: Det klassiska t-testet förutsätter att sigma för A och B kan antas vara lika (testet är dock relativt robust mot moderata skillnader).
Med hjälp av utökad matematisk analys med datorstöd är detta krav inte längre nödvändigt men man måste ange detta i menyn för t-test. Se också övningarna.

Alla förändringar som görs i indatarutorna registreras på sidans 'kommandoruta'. För att skapa data i R måste raderna manuellt kopieras in i R och aktiveras. Därefter kan analysen utföras.

Det finns två knappar som visar övningar och några texter (i pdf-format). Den blå länken visar exempel på graf som skapas av %t-test-makrot i Minitab.

••••

Rutan visar två fördelningar: blå är 'Process A' och grön är 'Process B'. (Om det bara syns en fördelning innebär det att bägge har samma parametrar.)

Med de två radioknapparna ovan fördelningarna är det möjligt att visa den totala fördelningen dvs blandningen av process A och B.
Denna motsvarar de histogram som visas i Minitab då nedanstående kommandon har körts. Om skillnaden mellan två fördelningarna är liten syns inte detta tydligt och därför är det nödvändigt att göra en mer formell analys.

••••

'Kopiera/Klistra in' raderna i rutan nedan till 'Session window' i Minitab vid "MTB >"-prompten och tryck sedan på [Enter]-knappen på tangentbordet.

Första två raderna simulerar data för den angivna övningen. övriga rader är förslag på analys och grafer.

Om värdet ändras i någon av indatarutorna visas ett antal radioknappar som skriver in motsvarande kommandon i rutan.

••••

De två sifferuppgifterna visar det teoretiska medelvärdet och den teoretiska standardavvikelsen (sigma) som når kunden då processen har nuvarande prestanda, dvs då bägge processerna (A och B) blandas.
När skillnaderna mellan process A och B minskar, minskar också totalspridningen (sigma).

Klicka på radioknappen "Visa gemensam fördelning" (över grafen) för att se fördelningen av resultat som når kunden.

••••

t-test är en statistisk metodik att jämföra två medelvärden från t.ex. två processer, maskiner, metoder, etc. Med 'medelvärden' menas här processernas bakomliggande men okända medelvärden:

"Har vi tillräckligt med data för att påstå att de två metoderna är olika eller beror skillnaderna bara på slumpmässig variation i mätvärdena?"

Analysen tar alltså hänsyn till variationen i mätvärdena så att man inte av misstag fattar fel beslut och säger att processerna är olika. Som mått på skillnaderna mellan processerna används skillnaden mellan två ur data beräknade medelvärden. Denna skillnad ställs alltså mot variationen i data.

'Paired t-test'. Ett vanligt exempel är att man vill jämföra två mått på samma enhet. Antag att man har två olika skomaterial och låter skolpojkar använda ett material på vänsterskon och ett annat material på högerskon. Då kan data bestå av skillnaden i slitage mellan vänster- och högerskon och frågan är då om skillnaden är noll dvs de två skomaterialen är lika starka.

••••