Medelv.:
Stand.:
Min:
Max:
Visa/dölj programkod för R
Visa/dölj kommentarer
Info, referenser, m.m...
-3.5σ
+3.5σ
Blå fördelning: processen Röd fördelning: medelvärden
![]()

![]()
![]()
12. Konfidensintervall för medelvärdet (I)
Denna sida innehåller exempel och övningar på konfidensintervall för μ.
![]()
Medelvärde ('my'):
Standardavvikelse ('sigma'):
Stickprovsstorlek (2 – 99):
Antal stickprov (2 – 100):
Konfidensnivå (0.50 – 0.99):
Fig 1...
Fig 2...
![]()
Rutorna innehåller parametervärden som används för att simulera data. En ändring registreras direkt i kommandorutan till höger:
Medelvärde ('my'): Utfallet i processen är normalfördelat med medelvärdet 'my'. 'my' är den okända parametern för vilken konfidensintervallet beräknas.
Standardavvikelse ('sigma'): Processens standardavvikelse är 'sigma'.
Stickprovsstorlek (2 – 99): Antal mätvärden per stickprov.
Antal stickprov (2 – 100): Antal stickprov som kan simuleras.
Konfidensnivå (0.50 – 0.99): Konfidensnivån (som är en sannolikhet) har begränsats.
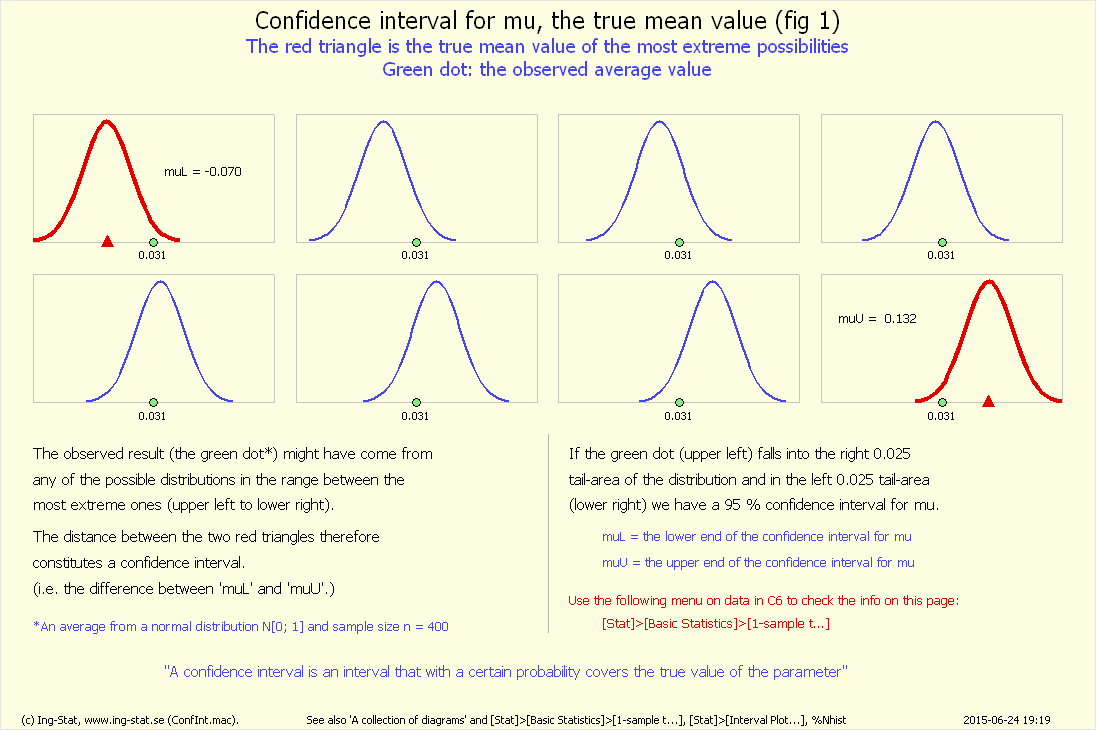
'Fig 1'...": visar två olika grafer.
Det finns knappar som visar övningar och texter (övningar i pdf-format kan skrivas ut och användas).
Alla förändringar som görs i indatarutorna registreras på sidans 'kommandoruta'. För att göra analys måste raderna manuellt kopieras in i analysprogrammet.
••••
Rutan visar två fördelningar:
• den blå är är processen
• den röda fördelningen av medelvärden
Bägge fördelningarna har – som förväntat – samma teoretiska medelvärde. Fördelningen för medelvärden har – också förväntat
– en mindre spridning, se formel under 'info'-knapp i den röda rutan.
(Eftersom ytan under de bägge kurvorna är 1, måste den röda fördelningen bli högre än den blå i diagrammet.)
De blå punkterna är simulerade värden med processens medelvärde ('my') och
standardavvikelse ('sigma'). Antal blå punkter är 'Stickprovsstorlek' * 'Antal stickprov'. Varje röd punkt är medelvärdet
av data i ett enskilt stickprov. Antal röda punkter är alltså 'Antal stickprov'.
••••
'Kopiera/Klistra in' raden i rutan nedan till 'Session window' i Minitab vid "MTB >"-prompten och tryck sedan på [Enter]-knappen på tangentbordet.
Kommandot startar ett Minitab-makro (%ConfIntWeb) med parametrar enligt indata till vänster. Med dessa uppgifter simuleras ett antal konfidensintervall. (De två sista siffrorna anger vilka grafer som skall skrivas ut av Minitab.)
Om värdet ändras i någon av indatarutorna ändras också motsvarande kommando i rutan.
••••
Siffrorna visar processens parametrar:
• det teoretiska medelvärdet
• den teoretiska standardavvikelsen (sigma)
• den teoretiska standardavvikelsen för medelvärdet
Uttrycket för standardavvikelsen för medelvärdet:
Det är altså tydligt att när n ökas så minskar medelvärdets standardavvikelse. Detta verkar naturligt eftersom mer data borde ge en bättre skattning av μ.
Den röda fördelningen visar medelvärdets variation. Om n ("Stickprovsstorlek...") ökas så blir den röda fördelningen smalare.
••••
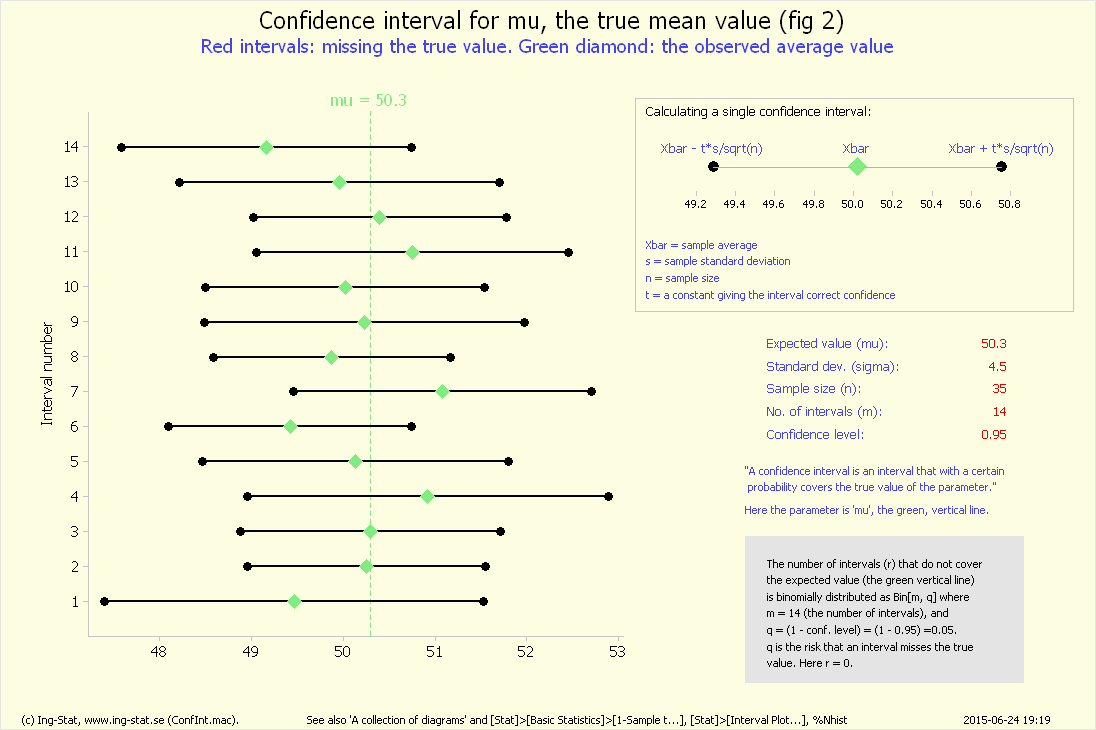
Allmänt. Denna övning handlar om konfidensintervall för μ och dess tolkning. Dylika intervall är vanliga inom statistisk analys och handlar om att 'fånga in' det sanna värdet på en okänd parameter, här μ-värdet.
Beräkning av intervallet. Många statistikprogram beräknar rutinmässigt intervallets ändpunkter och den formel som används här finns i PDF-dokumenten.
Tolkning av intervallet. även om ett intervall för μ anges enkelt som t.ex. '4.5−7.6' skall det tolkas som att 'intervallet av μ-värden 4.5−7.6 inte kan förkastas som möjliga värden på μ'.
••••