Medelv.:
Stand.:
Min:
Max:
Info, referenser, m.m...
![]()
Visa en fördelning per process
Visa gemensam fördelning

![]()
![]()
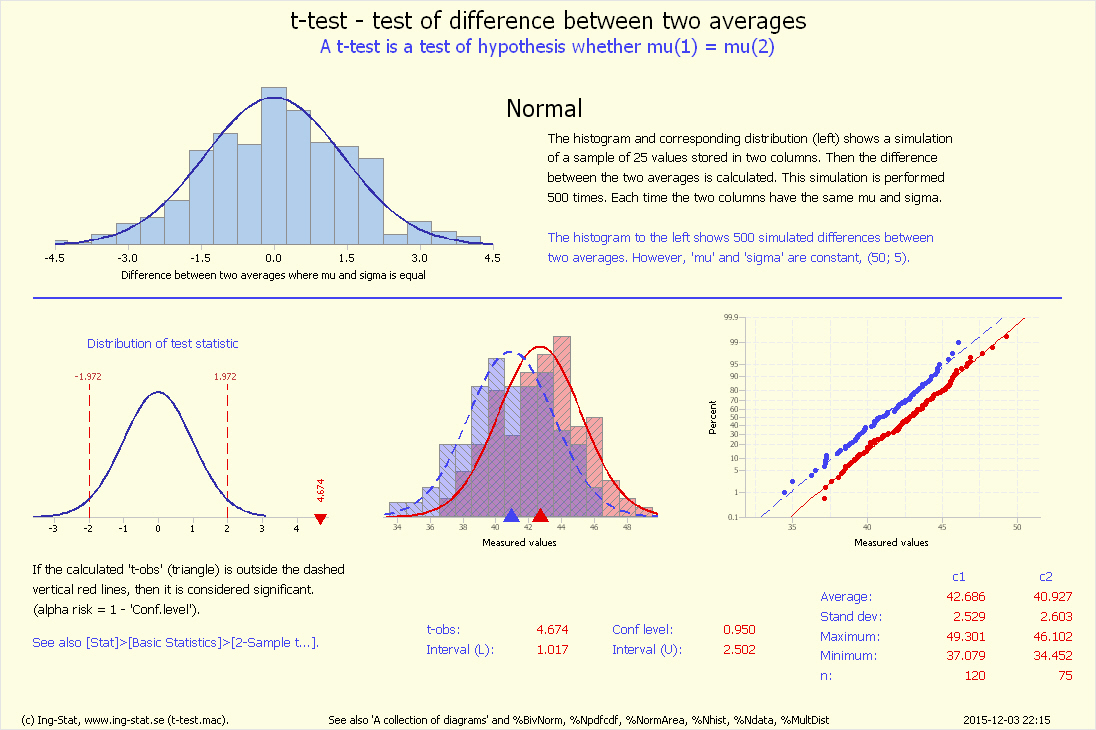
t-test – en jämförelse mellan medelvärden
"Är μA = μB eller μA ≠ μB"
Minitab-menyer...
Antal mätvärden process A:
Medelvärde process A:
Standardavvikelse process A:
Antal mätvärden process B:
Medelvärde process B:
Standardavvikelse process B:
Konfidensnivå (0.50 - 0.99):
Sigma antas lika i A och B
Använd %t-test-makrot
Använd Minitab-kommandon
Använd Mintab-menyer
%t-test...
%ttestnotOK...
![]()
![]()
Varje ruta innehåller parametervärden som används för att simulera data för analys (data skapas med makrot %ttestData). En ändring registreras direkt i rutorna till höger:
Antal mätvärden process A: Här anges antal mätvärden från process A.
Medelvärde process A: Här anges medelvärdet för process A.
Standardavvikelse process A: Här anges standardavvikelsen för process A.
Antal mätvärden process B: Här anges antal mätvärden från process B.
Medelvärde process B: Här anges medelvärdet för process B.
Standardavvikelse process B: Här anges standardavvikelsen för process B.
Konfidensnivå: Alla statistiska test har en sannolikhet (risk) att felaktigt ge 'signifikant resultat' dvs slumpmässig variation ger analysen ett felaktigt svar. Denna risk är (1 - konfidensnivå).
Sigma antas lika i A och B: Det klassiska t-testet förutsätter att sigma
för A och B kan antas vara lika (testet är dock relativt robust mot moderata skillnader).
Med hjälp av utökad matematisk analys med datorstöd är detta krav inte längre nödvändigt men man måste ange detta
i menyn för t-test (%t-test-makrot analyserar dock enligt 'klassigt krav'). Se också övningarna.
Alla förändringar som görs i indatarutorna registreras på sidans 'kommandoruta'. För att skapa data
i Minitab måste raderna '%ttestData...' manuellt kopieras in i Minitab och aktiveras. Därefter kan analysen utföras.
Det finns två knappar som visar övningar och några texter (i pdf-format). Den blå länken visar
exempel på graf som skapas av %t-test-makrot i Minitab.
••••
Rutan visar två fördelningar: blå är 'Process A' och grön är 'Process B'.
(Om det bara syns en fördelning innebär det att bägge har samma parametrar.)
Om markören förs över graffönstret visas en vertikal blå linje. Det visade värdet
är linjens läge på X-axeln.
Med de två radioknapparna ovan fördelningarna är det möjligt att visa den totala
fördelningen dvs blandningen av process A och B. Denna motsvarar de histogram som visas i Minitab då
nedanstående kommandon har körts. Om skillnaden mellan två fördelningarna är liten syns inte
detta tydligt och därför är det nödvändigt att göra en mer formell analys.
••••
'Kopiera/Klistra in' raderna i rutan nedan till 'Session window' i Minitab vid "MTB >"-prompten och tryck sedan på [Enter]-knappen på tangentbordet.
Första två raderna simulerar data för den angivna övningen. övriga rader är förslag på analys och grafer.
Om värdet ändras i någon av indatarutorna visas ett antal radioknappar som skriver in motsvarande kommandon i rutan.
••••
De två sifferuppgifterna visar det teoretiska medelvärdet och den teoretiska standardavvikelsen (sigma)
som når kunden då processen har nuvarande prestanda.
När skillnaderna mellan process A och B minskar
minskas också spridningen (sigma).
Klicka på radioknappen "Visa gemensam fördelning" (över grafen) för att se fördelningen av resultat som når kunden.
••••
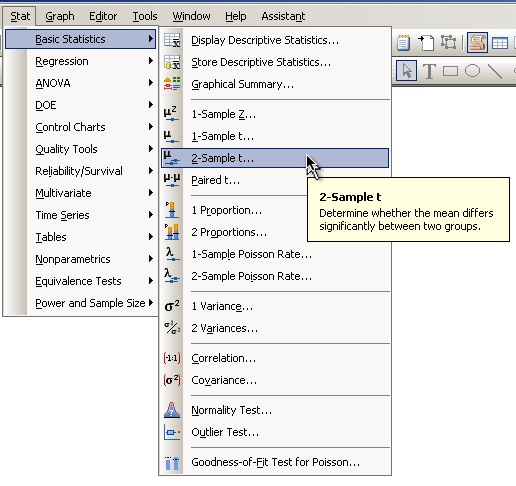
Meny för 't-test' av två datakolumner:
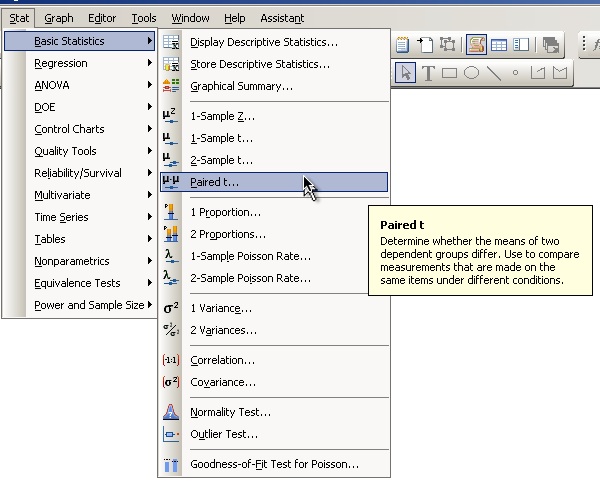
Meny för 'Paired t-test' av två datakolumner:
••••
Allmänt
Nedan finns ett antal övningar som analyserar data som simulerats med makrot %ttestData. Det finns flera sätt att analysera data (se radioknapparna):
- Med hjälp av makrot %t-test (som också genererar några grafer i Minitab)
- Med Minitab-kommandon (som skrivs ut i kommando-rutan)
- Med Minitabs egna menyer (som förstås ger fler möjligheter men kräver mer kunskap)
"Sigma antas..." - se info-knappen i parameterrutan till vänster för förklaring.
Klicka på övriga infoknappar för att förstå sidans information.
Övning 1 – en första körning (icke klickbar)
Initialt har de två processerna samma sigma (2.5) och en medelvärdesskillnad på exakt en sigma (43.0 - 42.5 = 2.5). Klicka radioknappen 'Visa gemensam...'
och se den totala fördelningen över blandningen av Process A och B.
En medelvärdesskillnad på en sigma måste anses vara stor och bör således elimineras. Trots storleken är det svårt eller omöjligt att från den totala
fördelningen upptäcka något onormalt.
Överför samtliga kommandona till Minitab-fönstret och tryck [Enter]. Studera grafen som skapas av %t-test-makrot.
Genomför också analysen dels med Minitabs kommandon och Minitabs menyer.
Övning 2 – 'Paired t-test' (klickbar)
I vissa situationer är det bättre att göra analysen som en s.k. 'paired t-test'.
Exempel: en konstruktör tillverkar en elektronisk 'grej' och han har två olika material för tillverkning av skyddskåpa. Han mäter alla 'grejorna' med kåpa 1
och kåpa 2. För varje par mätningar ('1' och '2') räknar han ut skillnaden och detta blir hans mätvärden.
(Kanske hans önskan är att visa att det inte finns någon skillnad och det är bra ty kåpa 2 är mycket billigare.
Kanske han hoppas att kåpa 1 ger signifikant bättre resultat ty den är hans egen konstruktion.
Skapa lika många mätvärden i två kolumner och använd sedan Minitabs menyer.
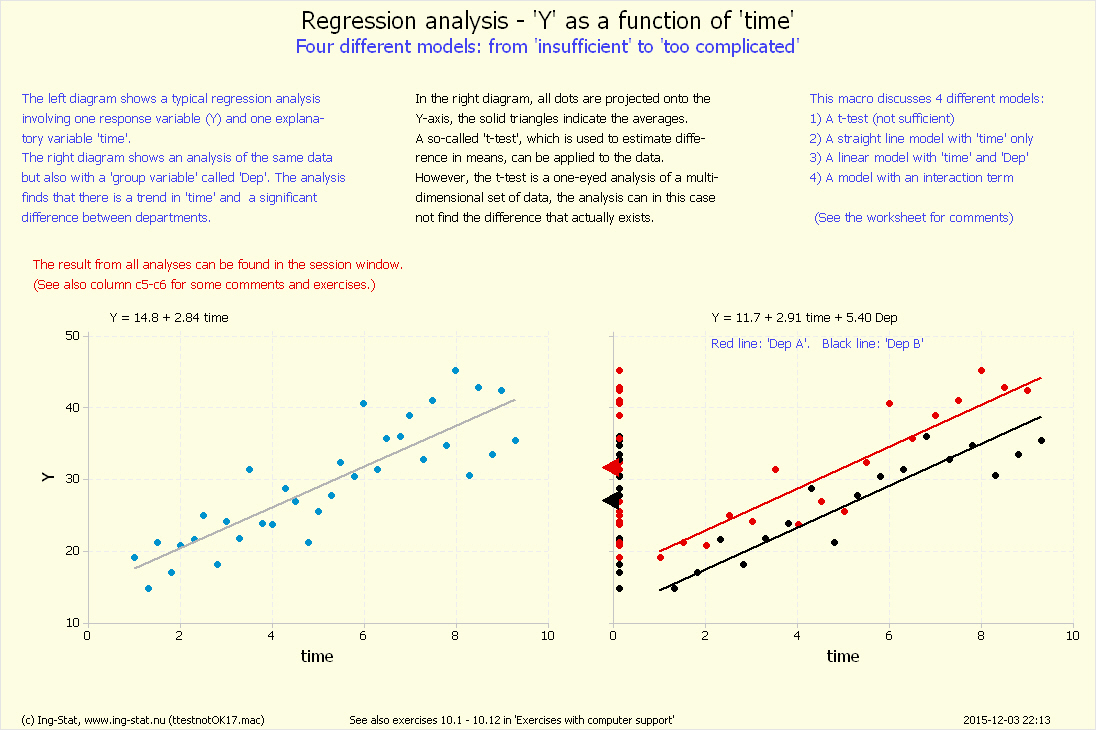
övning 3 – ibland är 't-test' fel! (klickbar)
Ett t-test kan ibland ge ett felaktigt eller otydligt resultat. Det kan finnas andra variabler som påverkar mätresultatet så att en verklig skillnad
inte fångas upp av analysen med ett t-test. Minitab-makrot %ttestnotOK17 visar på en sådan situation. (Obs att analysen involverar s.k. regressionsanalys).
Makrot (%ttestnotOK17) genererar egna data och använder sålunda inte någon indata från denna sida.
••••