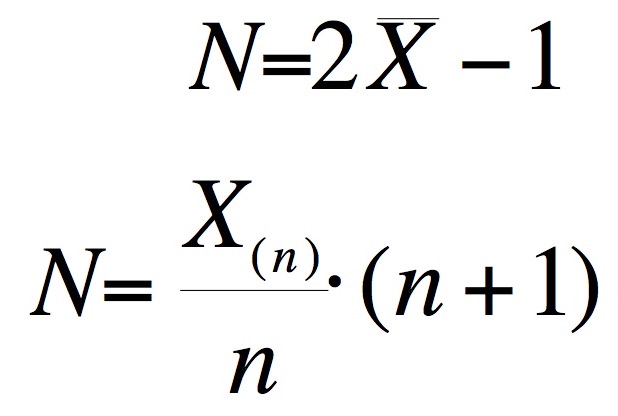
Visa/dölj simulerat resultat
Visa/dölj "Två histogram"
Visa/dölj parametrar
Info, referenser, m.m...

![]()
![]()
Hur stort är 'N' – två olika beräkningssätt
Ett smartare sätt att utnyttja datamängden
![]()
![]()
överskrift
textmetod1
textmetod2
Den vetenskapliga historien är full exempel där man stegvis vidgat kunnandet på något speciellt område. Inom matematik och matematisk statistik handlar det ofta om bevis. Det nya kan vara att en tidigare antagen restriktion visas vara onödig eller som exemplet i detta program, en annan skattning som visar sig ha mindre variation.
Exemplet i simuleringen beskrivs i litteraturen ibland som 'taxiproblemet' men också en metod under 2:a världskriget då man försökte skatta fiendens samlade styrkor inom något speciellt vapenslag.
Simuleringen skapar en dataserie från 1 till N (N anges med den översta slidens högra handtag). Därefter tas ett stickprov om n enheter (utan återläggning) från serien. Från dessa n värden skattas N med de två olika matematiska uttrycken som presenteras på sidan.
Skattning 1. Skattning 1 är ganska lätt att själv härleda. En vanlig tärning har det teoretiska medelvärdet 3.5.
Två gånger detta ger 7 och en '-1' justerar resultatet till rätt värde (6).
Skattning 2. X(n)/n ger medelavstånden mellan observationerna. Om detta adderas till X(n) erhålles, efter lite matematisk
manipulation, X(n)/n*(n + 1). Antag att N = 6 (som en tärning) och att n = 6, dvs alla värdena. Då erhålles 6/6*(6+1) som blir 7. Genom att subtrahera
'-1' erhålles N = 6.
Variationen. Det mest iögonfallande är den stora skillnaden i skattningarnas variation. En sökning på nätet av
'the German tank problem' ger mer information och fler aspekter på problemet, dess formulering och olika lösningsförslag.
Variansreducerande metoder. Metoder för att reducerat variationen i skattningar brukar med ett samlingsnamn
kallas variansreducerande metoder. Inte sällan betyder det att lägga upp en undersökning på ett smartare sätt.
Visa/dölj simulerat resultat: det simulerade utfallet kan döljas eller visas.
Det kan också stängas med dialogrutans vanliga kryss.
Visa/dölj "Två histogram": rutan med några exempel
kan döljas eller visas men kan också stängas med dialogrutans vanliga kryss.
Visa/dölj parametrar: dialogrutan med slider för parametervärden kan döljas eller visas men kan också stängas med dialogrutans vanliga kryss.
Repetera simulering: genomför en ny simulering med de inställda parametervärdena.
••••
Översta talaxeln. Den översta axeln visar med gröna fyllda cirklar läget på de nummer som dragits ur serien
1, 2, 3, ...N.
Mellersta talaxeln. Den mellersta axeln visar med ljusblå fyllda cirklar läget på alla skattningar av N
med 'metod 1'.
Understa talaxeln. Den understa axeln visar med röda fyllda cirklar läget på alla skattningar av N
med 'metod 2'.
••••
Sliderna anger parametervärdena för beräkningen. En beräkning sker kontinuerligt då sliden flyttas.
Stickprov ('n' ur 'N'):
Parametern n anger hur många enheter som dras utan återläggning ur populationen som består av N enheter.
Totalt antal enheter ('N'):
Denna population består av siffrorna 1, 2, 3, ...N.
Antal upprepningar:
Anger antal gånger som ett stickprov dras. Varje sådant stickprov ger ett värde som illustreras med ljusblå respektive röd fylld cirkel.
Gränser histogram (+/-):
De två gränserna på histogrammens X-axel kan ändras så att histogrammen bättre fyller ut X-axeln.
••••
Histogram över skattningarna av N
Histogrammen visar att de två skattningarna har väldigt olika egenskaper.
Medan den översta visar stor spridning
och ett relativt symmetriskt utfall, visar den undre skattningen en negativ skevhet utfall.
Men trots det är antagligen skattning två bäst att använda.
Det är dock viktigt att veta att i allmänhet så finns det många krav på en skattning och ofta finns det en konflikt mellan dessa krav.
••••