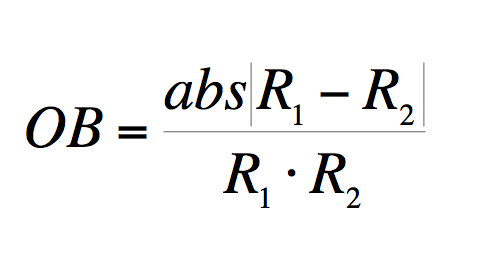
Visa/dölj histogram för obalans
Visa/dölj simulering av obalans
Visa/dölj parametrar
Info, referenser, m.m...

![]()
![]()
Simulering av obalans i en elektronisk krets
"Hur stor är risken att en krets inte är godkänd?"
![]()
text på histogram 1
text på histogram 2
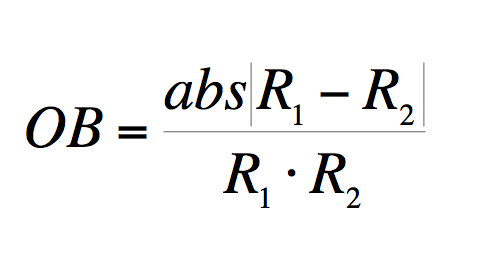
Sigma mOhm
Felprocent utanför
'Gränsvärde obalans'
Simulering av obalans OB:
'sigma (L)' och 'sigma (H)'
Gränsvärde obalans
Antal steg (L) till (H)
Antal replikat per sigma
Antal (n) per simulering
Min o max Y-axeln (felprocent)
Max X-axeln (histogram)
Antal per histogram
Variationen i ett system är i allmänhet kumulativ dvs den ökar då fler och fler komponenter adderas till systemet. Detta gäller även t.ex. i processer med olika tidskomponenter, men också i mekaniska eller elektroniska system.
Ibland är variationen ganska enkelt additiv och totalvariationen erhålles som en enkel summa. Detta gäller i åtminstone enkla mekaniska komponenter. Inte sällan är dock totalvariationen en mer komplicerad funktion som t.ex. i formeln nedan:
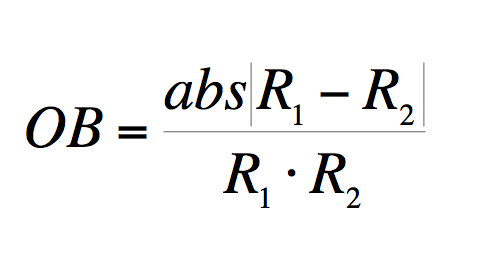
Formeln uttrycker obalans i en krets där obalansen uppstår då det tyvärr
ibland är en skillnad i resistans mellan de två komponenterna.
Skillnaden i resistans kommer av att det finns en viss variation (uttryckt här som sigma (standardavvikelse)) i tillverkningen av komponenter.
Naturligtvis kan en viss obalans tolereras, denna tolerans anges med sliden för gränsvärdet. Vilken sigma är nödvändigt för att få en felkvot
som är acceptabel?
Det kan vara en ganska svår uppgift att matematiskt teoretiskt bestämma felkvot vid givet gränsvärde. Därför kan simulering ofta vara ett
verktyg för att belysa situationen och lösa problemet på ett sätt som är acceptabelt för alla inblandade.
Visa/dölj histogram för obalans: de två histogrammen kan döljas eller visas.
Det kan också stängas med dialogrutans vanliga kryss.
Visa/dölj simulering av obalans: dialogrutan med simuleringen av obalans
kan döljas eller visas men kan också stängas med dialogrutans vanliga kryss.
Visa/dölj parametrar: dialogrutan med slider för parametervärden
kan döljas eller visas men kan också stängas med dialogrutans vanliga kryss.
[Kommentarer och övn]: visar ett antal kommentarer och övningar.
[Repetera simulering]: ett klick på knappen gör en ny simulering med de inställda parametervärdena.
••••
Sliderna anger parametervärdena för simuleringen. En ny simulering sker efter att en slid har förflyttats.
'Sigma (L)' och 'Sigma (H)':
X-axeln anger vilka sigma som använts för resistansen i de två komponenterna i kretsen. Simuleringen sker i steg mella 'Sigma (L)' och 'Sigma (L)'.
Gränsvärde obalansen:
En konstant som anger gränsen för obalans (OB) innan kretsen betraktas som 'ej OK'.
Antal steg (L) till (H):
Anger antal delsteg från lägsta sigma till högsta sigma.
Antal (n) per simulering: Varje punkt i diagrammet är felkvoten som simulerats med n värden. ('Fel'
är en krets med OB som överstiger gränsvärdet. OB beräknas med angiven formel (se huvudsidan eller dess 'info'-knapp).
Antal per histogram: De två histogrammen är separata simuleringar och antal värden
per histogram anges med sliden. Histogrammen anger beräknad obalans (Se formel). Det översta histogrammet är simulerat med lägsta sigma (på X-axeln i
huvuddiagrammet) och det understa diagrammet är simulerat med högsta sigma.
Min o max på Y-axeln (felprocent): För att resultatet i huvuddiagrammet skall
presenteras tillfredsställande kan Y-axelns ändpunkter ändras.
Max X-axeln (histogram): Ändrar max-värdet på histogrammens X-axel.
••••
Två histogram för simulerade obalansvärden.
Histogrammen visar simulerade obalans-värden (se formel). Det övre histogrammet
visar värden som simulerats med lägsta sigma på de två komponenterna i kretsen. På motsvarande sätt är det undre histogrammet simulerat med högst sigma
som är inställt på sliden 'sigma...'. Eftersom det undre histogrammet har större spridning är det samtidigt lägre än det övre.
De vertikala röda linjerna är gränsvärdet (toleransen) för obalans i kretsen. Gränsvärdet
ändras med sliden 'Gränsvärde...' Dessutom visas beräknad felprocent för övre respektive undre histogrammet samt antal värden i histogrammet.
De två felprocenterna överensstämmer (ungefär) med ändpunkterna i den streckade kurvan i huvuddiagrammet.
••••
Diagrammet visar simulering av obalans i kretsar där felprocenten (Y) plottas mot sigma (X).
En s.k. logistisk regressionsmodell har anpassats till data och ritas som en streckad röd linje. (Logistisk regression modellerar felkvot mot olika typer av förklaringsvariabel där 'sigma' är förklaringsvariabel i denna modell.)
Y-axeln visar felprocenten och ändpunkterna kan ändras med sliden 'Min o max...'. X-axeln visar sigma mOhm vars lägsta och högsta värde regleras med sliden 'sigma (L)...' och antal delsteg ändras med 'Antal steg...'. För varje sigma har ett antal simuleringar gjorts (ändras med sliden 'Antal replikat...'. (Notera att det kan bli flera punkter i samma Y-läge). antal kvarvarande rapporter medan X-axeln visar en tidsaxel i dagar.
Om datormarkören förs över diagrammet ändras den till ett hårkors och punktens läge anges strax ovanför hårkorset.
••••