*
De blå punkterna är skillnaderna mellan 'Hål' och 'Axeltapp' och har sålunda samma skala som den blå fördelningen.
Medelv.:
Stand.:
Min:
Max:
Info, referenser, m.m...
![]()
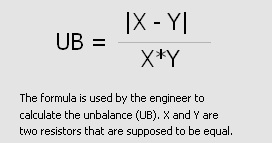
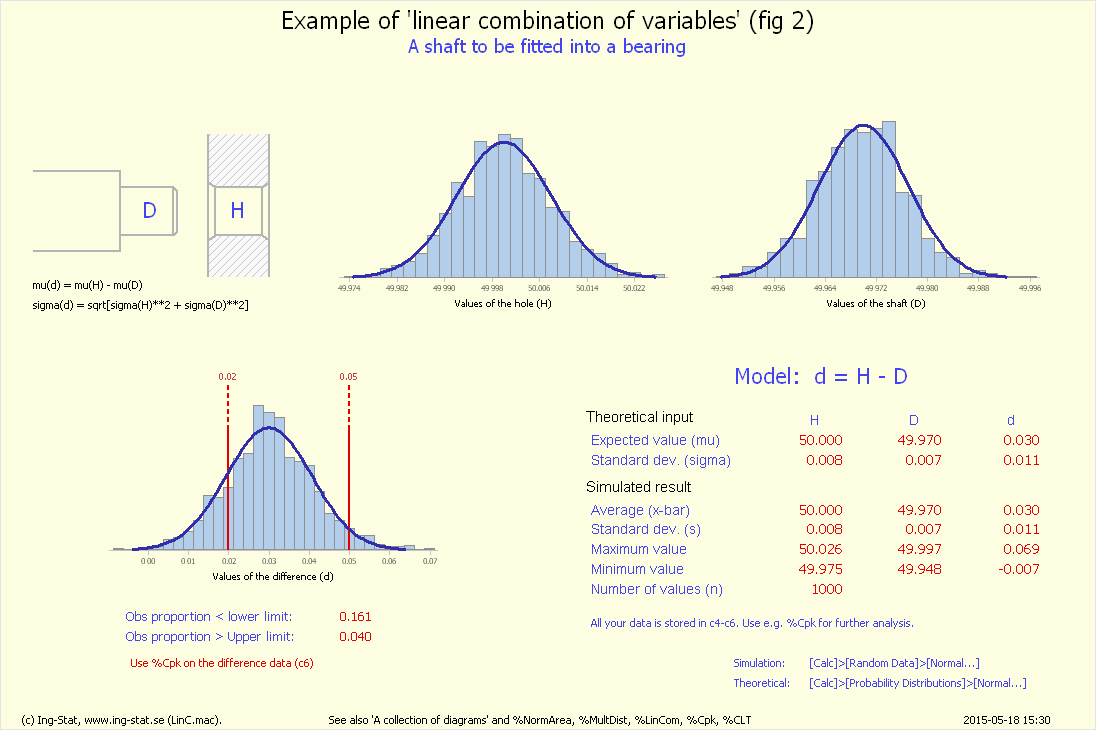
Fördelningen är skillnaden (d): 'd = Hål - Axeltapp'

![]()
![]()
Linjära och icke-linjära kombinationer av variabler
![]()
Antal enheter att simulera:
Medelvärde hål (H):
Standardavvikelse hål:
Medelvärde axeltapp (D):
Standardavvikelse axeltapp:
Undre toleransgräns:
Övre toleransgräns:
Visa 'fig 1' i Minitab
Visa 'fig 2' i Minitab
%LinC (fig 1)...
%LinC (fig 2)...
![]()
Varje ruta innehåller parametervärden som används för att simulera data för analys (data skapas med makrot %LinCweb). En ändring registreras direkt i kommandorutan till höger:
Antal enheter att simulera: Värdet anger hur många 'axeltapp/hål'-enheter som simuleras för beräkningar, histogram, etc.
Medelvärde hål (H): Här anges teoretiskt medelvärde för det bearbetade hålet.
Standardavvikelse för hål: Här anges hålets standardavvikelse (3 decimaler).
Medelvärde axeltapp (D): Här anges teoretiskt medelvärde för den bearbetade axeltappen.
Standardavvikelse för axeltapp: Här anges axeltappens standardavvikelse (3 decimaler).
Undre toleransgräns: Här anges undre toleransgräns för (d), dvs skillnaden mellan hål och axeltapp.
Övre toleransgräns: Här anges övre toleransgräns för (d), dvs skillnaden mellan hål och axeltapp.
Visa 'fig 1' i Minitab: Makrot %LinCweb i Minitab skapar två grafer. Här anges om den första grafen skall visas.
Visa 'fig 2' i Minitab: Makrot %LinCweb i Minitab skapar två grafer. Här anges om den andra grafen skall visas.
Övrigt: Det finns tre knappar som visar övningar och texter (övningar i pdf-format kan skrivas ut och användas). De tre blå länkarna visar exempel på grafer som skapas av %LinC-makrot i Minitab.
Alla förändringar som görs i indatarutorna registreras på sidans 'kommandoruta'. För att skapa data i Minitab måste raden '%LinCweb...' manuellt kopieras in i Minitab och aktiveras. Därefter kan analysen utföras.
••••
Rutan visar en teoretisk normalfördelning för (d), skillnaden 'Hål - Axeltapp'.
Längst till vänster respektive höger visas de två toleransgränserna och fördelningens väntevärde visas med en vertikal prickad linje.
De numeriska värdena ('my' och 'sigma' och 'cpk') anges i rött i rutan till vänster.
Under fördelningen finns simulerade för 'Hål' respektive 'Axeltapp' (Röd respektive Grön). De blå punkterna är skillnaden mellan hål och axeltapp och sålunda samma skala som den blå, teoretiska fördelningen.
••••
Denna ruta innehåller kommandon för statistikprogrammet Minitab. Kommandona måste överföras manuellt:
• Klicka någonstans i kommandorutan
• Markera allt (CTL/A)
• Kopiera allt (CTL/C)
• Öppna Minitab
• Klistra in allt vid MTB > (CTL/V)
• Tryck ENTER för aktivera kommandona
••••
Siffrorna visar följande för spelet mellan 'Hål' och 'Axeltapp':
• det teoretiska medelvärdet
• den teoretiska standardavvikelsen (sigma)
• 'Cpk'-värdet
för resultat som når kunden med nuvarande process.
Medelvärde och standardavvikelse för spelet blir:
Cpk-värdet beräknas på vanligt sätt, se t.ex. sidan för 'Cpk'-analys.
••••
Övning 4 – 7 handlar om ’icke-linjära kombinationer’. Ibland kan det vara lätt att identifiera en dylik situation, ibland lite svårare och det underlättas inte av att definitioner är en smula otydliga. (Ibland kallas en enkel krökt regressionskurva felaktigt för icke-linjär. Och vad skall man kalla t.ex. en binomialfördelad variabel där ’p’ självt betraktas som en variabel?)
För att få åtminstone en approximation av väntevärde och varians kan man använda Gauss approximationsformler. Dessa är väl värda att studera och kunna, se litteraturen eller nätet för detaljer. Inom matematiken används ibland uttrycket change of variables och om man vill ha exakta utrryck för väntevärde, varians, fördelning, osv måste man använda avancerad matematik.
Det ibland självklara är inte alltid så självklart:
Det första uttrycket visar att om man vill ha väntevärdet av den inverterade variabeln (vänstra ledet) så går det inte att beräkna väntevärdet E(X) i högra ledet och sedan invertera detta. Annan metodik behövs.
Det andra uttrycket visar att om man vill ha variansen av produkten av två variabler (vänstra ledet) så går det inte att beräkna de två varianserna (högra ledet) och ta produkten av dessa. Annan metodik behövs.
••••
Övning 1 – simulering av skillnaden (d) mellan 'Hål' och 'Axeltapp'
Indata simulerar 200 lagerenheter som består av 'hål' och 'axeltapp'. Skillnaden mellan dessa är den intressanta variabeln. Överför kommandona till
Minitab-fönstret och tryck [Enter]. Grafen märkt 'fig 1' innehåller formler o.d. och graf märkt 'fig 2' sammanfattar mätningarna.
(Exempel på graferna finns via länkarna nederst på sidan.) Notera att fördelningen av differenser på 'fig 2' motsvarar den teoretiska fördelningen på denna sida.
Övning 2 – centrera processen
Utgå ifrån övning 1. Ändra något av medelvärdena (eller bägge) så att processen centreras mellan gränsvärdena. Kopiera kommandona till Minitab och verifiera i 'fig 2' att mätresultaten för 'd'
är centrerade. (Obs genom att 'klicka bort' 'fig 1' visas bara 'fig 2' i Minitab.)
Övning 3 – minska variationen
Utgå ifrån övning 2. Om variationen i 'Hål' respektive 'Axeltapp' är alltför hög blir slutresultatet inte inom specifikationerna. Minska de två standardavvikelserna (samma värde i bägge, tre decimaler)
så att all variation faller inom toleransgränserna. Kör en simulering i Minitab och verifiera resultatet.
Övning 4 – Pythagoras sats
Pythagoras sats är välkänd från grundläggande matematik. 'Hypotenusans längd är lika med kvadratroten ur summan av kvadraterna på de två kateterna'.
Alltså är hypotenusans längd en icke-linjär kombination av kateternas längder.
Om kateternas 'sigma' är litet i förhållande till deras väntevärde 'my', blir hypotenusans längd approximativt normalfördelad. (Ändra värdena i
kommandorutan och gör en ny simulering. Det är dock inte självklart hur hypotenusans 'sigma' och väntevärde beräknas.) Jämför också med övning 5.
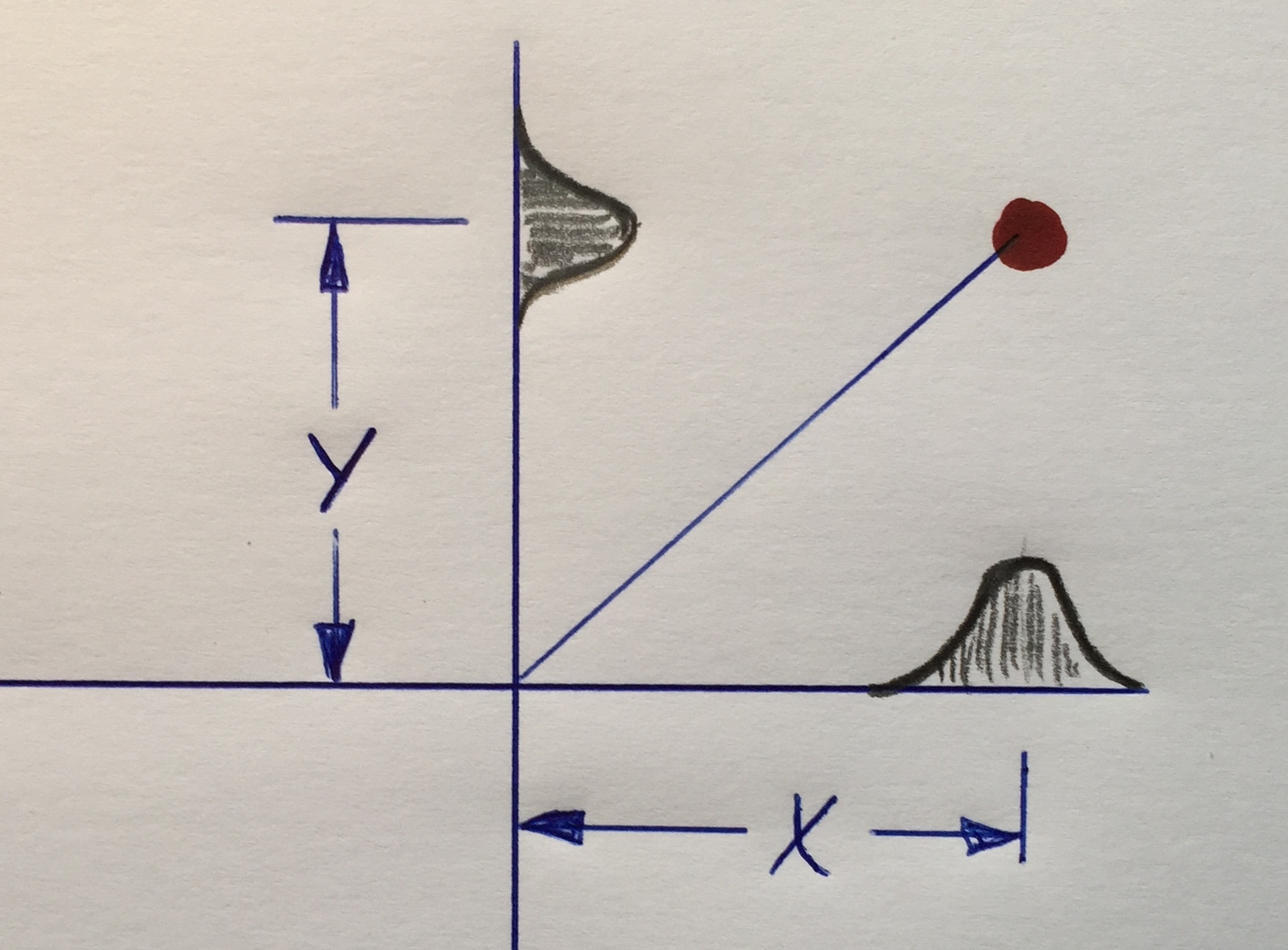
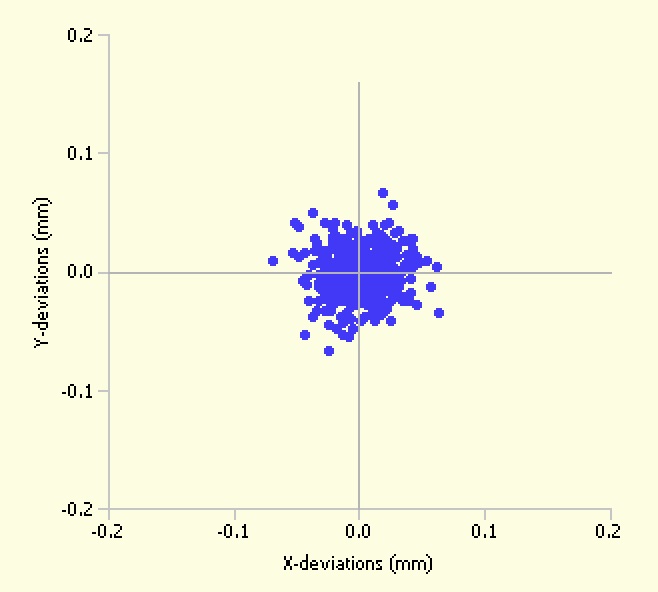
Övning 5 – radiell avvikelse
En radiell avvikelse i planet i ett vanligt koordinatsystem beräknas med hjälp av Pythagoras sats. Om kateterna (X och Y) är normalfördelade
med 'my' = 0 och standardavvikelsen 'sigma' (samma 'sigma' för både X och Y) blir den radiella avvikelsen Rayleighfördelad, ett specialfall av
Webullfördelningen med formparameter ('Shape') = 2 (använd kommandona för att verifiera detta).
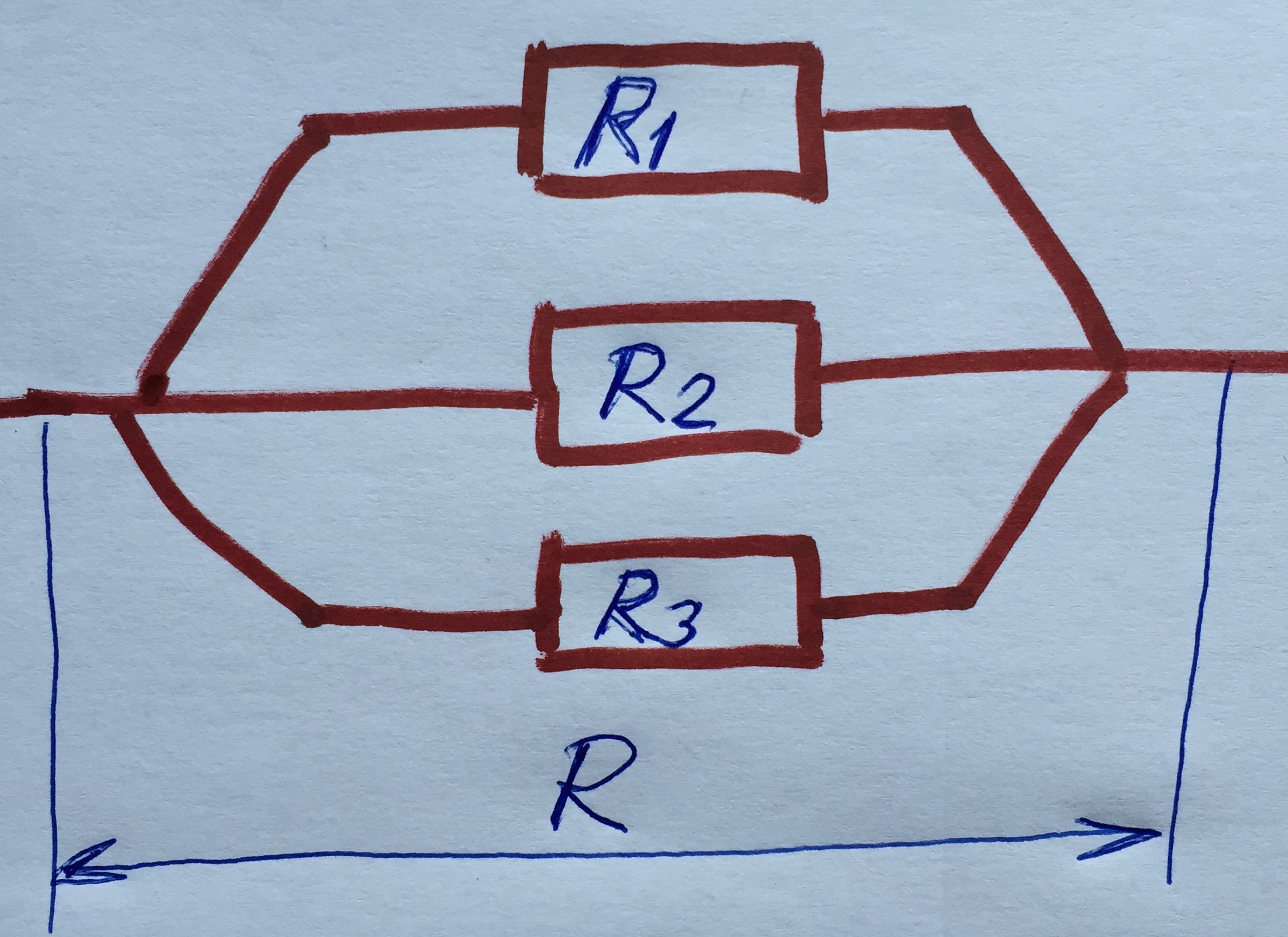
Övning 6 – parallellkopplade resistanser
Parallellkopplade komponenter är vanliga i elektroniska kretsar. Belysningspunkter i elnät i ett vanligt hus är parallellkopplade (en enkel julgransbelysning
är ofta seriekopplad).
För att beräkna den totala resistansen (R) över en krets måste den angivna formeln användas.
Övning 7 – obalans i en krets
Formeln är ett urklipp från makrot %SimUB. Formeln visar att om X = Y blir obalansen (UB) noll men om X och Y är olika blir det en viss obalans i kretsen.
Konstruktören har angivit att max 1% av alla kretsar får ha en obalans > 0.002. Vilket 'sigma' behövs för att tillfredsställa kravet? Pröva olika 'sigma', öka
eventuellt antal simulerade värden för att få entydigare bild. Kör också Minitab-makrot %SimUNB.
••••