Info, referenser, m.m...
![]()
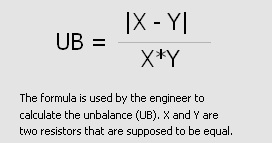
Fördelningen gäller skillnaden (d) 'Hål - Axeltapp'

![]()
![]()
Linjära och icke-linjära kombinationer av variabler
![]()
Antal enheter att simulera:
Medelvärde hål (H):
Standardavvikelse hål:
Medelvärde axeltapp (D):
Standardavvikelse axeltapp:
Undre toleransgräns:
Övre toleransgräns:
Visa 'fig 1' i Minitab
Visa 'fig 2' i Minitab
%LinC (fig 1)...
%LinC (fig 2)...
![]()
Varje ruta innehåller parametervärden som används för att simulera data för analys (data skapas med makrot %LinCweb). En ändring registreras direkt i kommandorutan till höger:
Antal enheter att simulera: Värdet anger hur många 'axeltapp/hål'-enheter som simuleras för beräkningar, histogram, etc.
Medelvärde hål (H): Här anges teoretiskt medelvärde för det bearbetade hålet.
Standardavvikelse för hål: Här anges hålets standardavvikelse (3 decimaler).
Medelvärde axeltapp (D): Här anges teoretiskt medelvärde för den bearbetade axeltappen.
Standardavvikelse för axeltapp: Här anges axeltappens standardavvikelse (3 decimaler).
Undre toleransgräns: Här anges undre toleransgräns för (d), dvs skillnaden mellan hål och axeltapp.
Övre toleransgräns: Här anges övre toleransgräns för (d), dvs skillnaden mellan hål och axeltapp.
Visa 'fig 1' i Minitab: Makrot %LinCweb i Minitab skapar två grafer. Här anges om den första grafen skall visas.
Visa 'fig 2' i Minitab: Makrot %LinCweb i Minitab skapar två grafer. Här anges om den andra grafen skall visas.
Övrigt: Det finns tre knappar som visar övningar och texter (övningar i pdf-format kan skrivas ut och användas). De tre blå länkarna visar exempel på grafer som skapas av %LinC-makrot i Minitab.
Alla förändringar som görs i indatarutorna registreras på sidans 'kommandoruta'. För att skapa data i Minitab måste raden '%LinCweb...' manuellt kopieras in i Minitab och aktiveras. Därefter kan analysen utföras.
••••
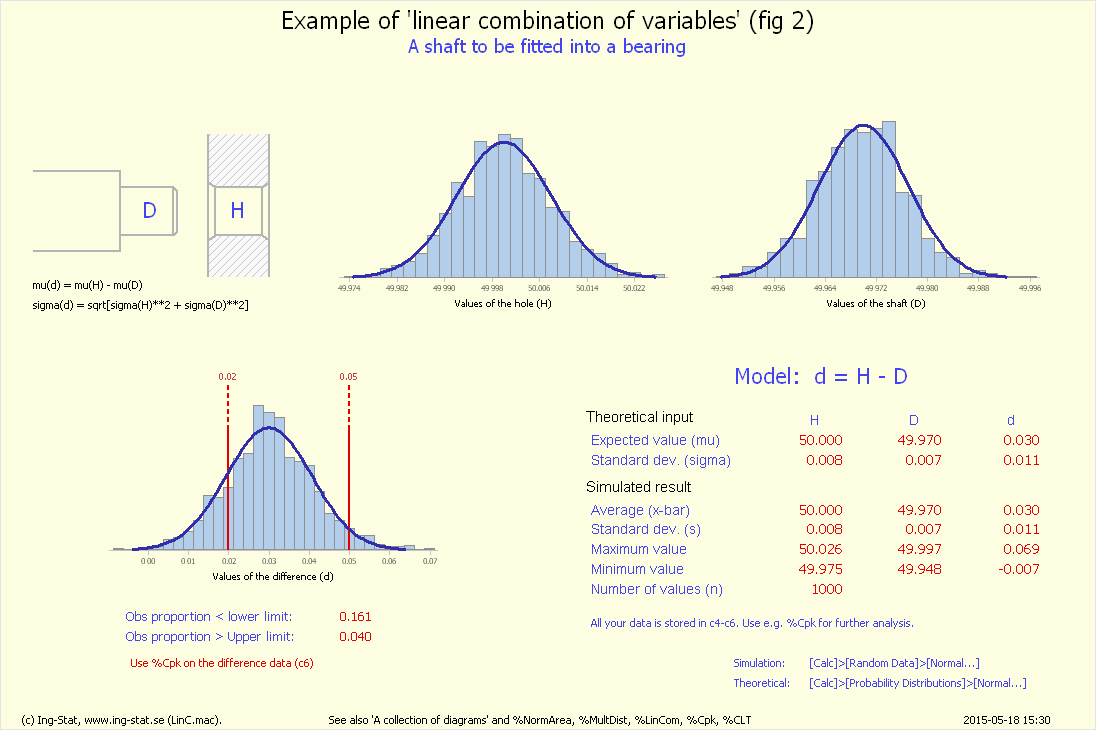
Rutan visar en teoretisk normalfördelning för (d), skillnaden 'Hål - Axeltapp'.
Längst till vänster respektive höger visas de två toleransgränserna.
Fördelningens väntevärde visas med en vertikal prickad linje.
De numeriska värdena ('my' och 'sigma' och 'cpk') anges i rött i rutan till vänster.
••••
Denna ruta innehåller kommandon för statistikprogrammet Minitab. Kommandona måste överföras manuellt:
• Klicka någonstans i kommandorutan
• Markera allt (CTL/A)
• Kopiera allt (CTL/C)
• Öppna Minitab
• Klistra in allt vid MTB > (CTL/V)
• Tryck ENTER för aktivera kommandona
••••
Siffrorna visar följande för spelet mellan 'Hål' och 'Axeltapp':
• det teoretiska medelvärdet
• den teoretiska standardavvikelsen (sigma)
• 'Cpk'-värdet
för resultat som når kunden med nuvarande process.
Medelvärde och standardavvikelse för spelet blir:
Cpk-värdet beräknas på vanligt sätt, se t.ex. sidan för 'Cpk'-analys.
••••
Övning 4 – 7 handlar om ’icke-linjära kombinationer’. Ibland kan det vara lätt att identifiera en dylik situation, ibland lite svårare och det underlättas inte av att definitioner är en smula otydliga. (Ibland kallas en enkel krökt regressionskurva felaktigt för icke-linjär. Och vad skall man kalla t.ex. en binomialfördelad variabel där ’p’ självt betraktas som en variabel?)
För att få åtminstone en approximation av väntevärde och varians kan man använda Gauss approximationsformler. Dessa är väl värda att studera och kunna, se litteraturen eller nätet för detaljer. Inom matematiken används ibland uttrycket change of variables och om man vill ha exakta utrryck för väntevärde, varians, fördelning, osv måste man använda avancerad matematik.
Det ibland självklara är inte alltid så självklart:
Det första uttrycket visar att om man vill ha väntevärdet av den inverterade variabeln (vänstra ledet) så går det inte att beräkna väntevärdet E(X) i högra ledet och sedan invertera detta. Annan metodik behövs.
Det andra uttrycket visar att om man vill ha variansen av produkten av två variabler (vänstra ledet) så går det inte att beräkna de två varianserna (högra ledet) och ta produkten av dessa. Annan metodik behövs.
••••
Övning 1 – simulering av skillnaden (d) mellan 'Hål' och 'Axeltapp'
Indata simulerar 1000 lagerenheter som består av 'hål' och 'axeltapp'. Skillnaden mellan dessa är den intressanta variabeln. Överför kommandona till
Minitab-fönstret och tryck [Enter]. Grafen märkt 'fig 1' innehåller formler o.d. och graf märkt 'fig 2' sammanfattar mätningarna.
(Exempel på graferna finns via länkarna nederst på sidan.) Notera att fördelningen av differenser på 'fig 2' motsvarar den teoretiska fördelningen på denna sida.
Övning 2 – centrera processen
Utgå ifrån övning 1. Ändra något av medelvärdena (eller bägge) så att processen centreras mellan gränsvärdena. Kopiera kommandona till Minitab och verifiera i 'fig 2' att mätresultaten för 'd'
är centrerade. (Obs genom att 'klicka bort' 'fig 1' visas bara 'fig 2' i Minitab.)
Övning 3 – minska variationen
Utgå ifrån övning 2. Om variationen i 'Hål' respektive 'Axeltapp' är alltför hög blir slutresultatet inte inom specifikationerna. Minska de två standardavvikelserna (samma värde i bägge, tre decimaler)
så att all variation faller inom toleransgränserna. Kör en simulering i Minitab och verifiera resultatet.
Övning 4 – Pythagoras sats
Pythagoras sats är välkänd från grundläggande matematik. 'Hypotenusans längd är lika med kvadratroten ur summan av kvadraterna på de två kateterna'.
Alltså är hypotenusans längd en icke-linjär kombination av kateternas längder.
Om kateternas 'sigma' är litet i förhållande till deras väntevärde 'my', blir hypotenusans längd approximativt normalfördelad. (Ändra värdena i
kommandorutan och gör en ny simulering. Det är dock inte självklart hur hypotenusans 'sigma' och väntevärde beräknas.) Jämför också med övning 5.
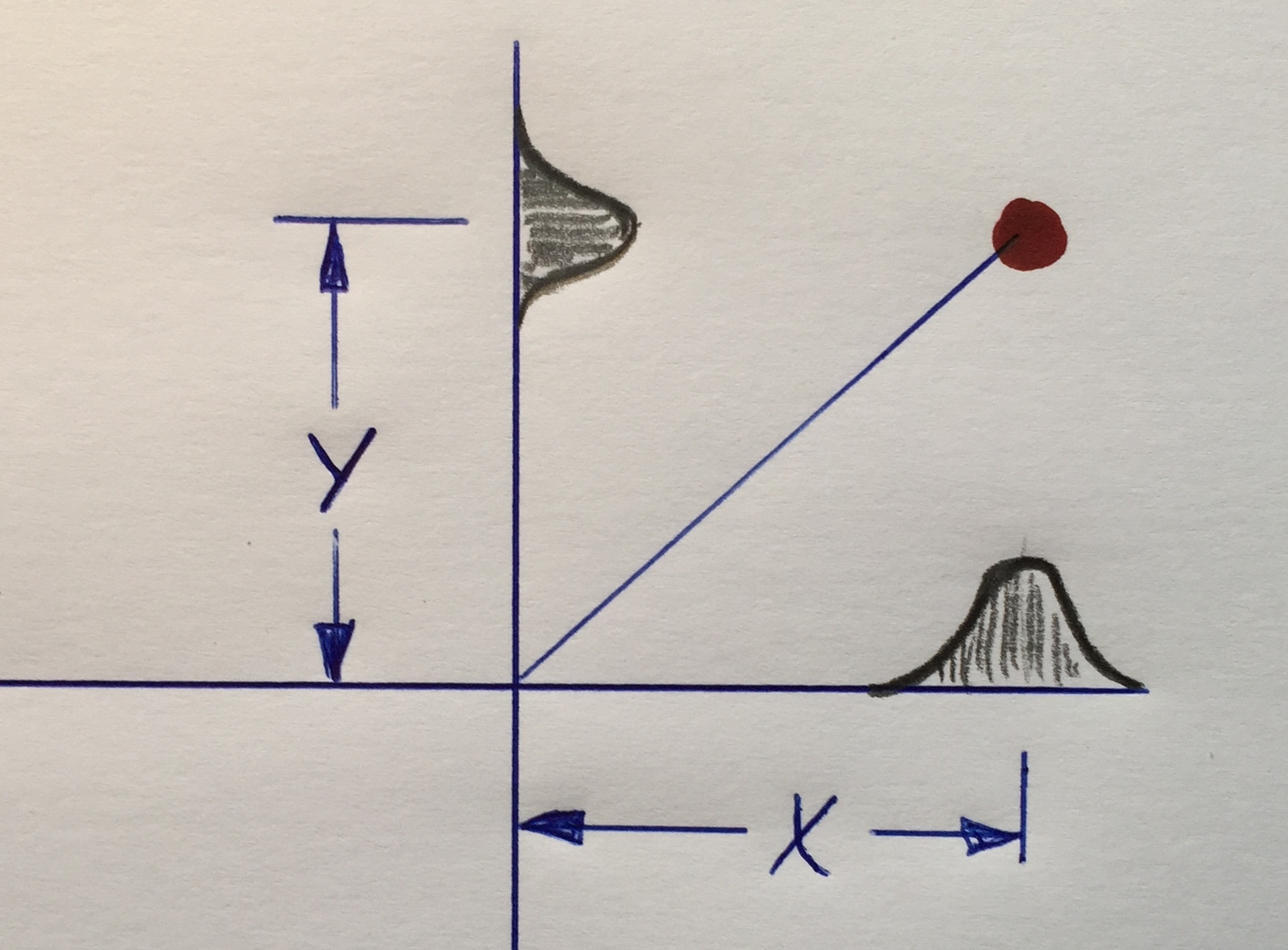
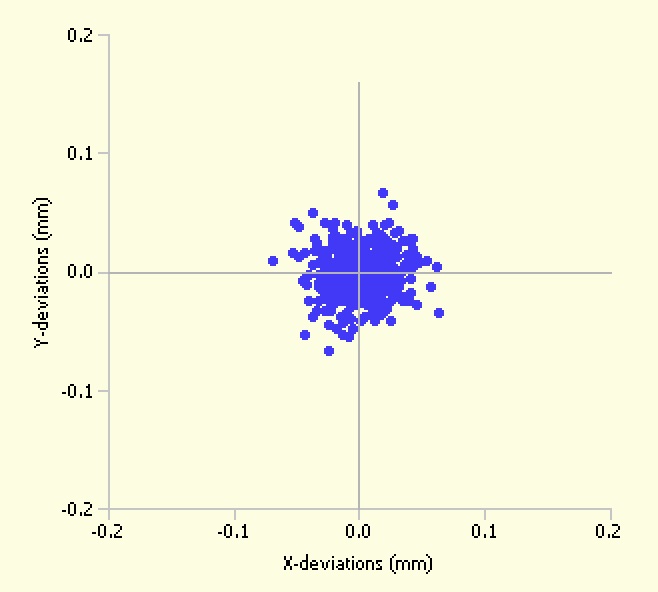
Övning 5 – radiell avvikelse
En radiell avvikelse i planet i ett vanligt koordinatsystem beräknas med hjälp av Pythagoras sats. Om kateterna (X och Y) är normalfördelade
med 'my' = 0 och standardavvikelsen 'sigma' (samma 'sigma' för både X och Y) blir den radiella avvikelsen Rayleighfördelad, ett specialfall av
Webullfördelningen med formparameter ('Shape') = 2 (använd kommandona för att verifiera detta).
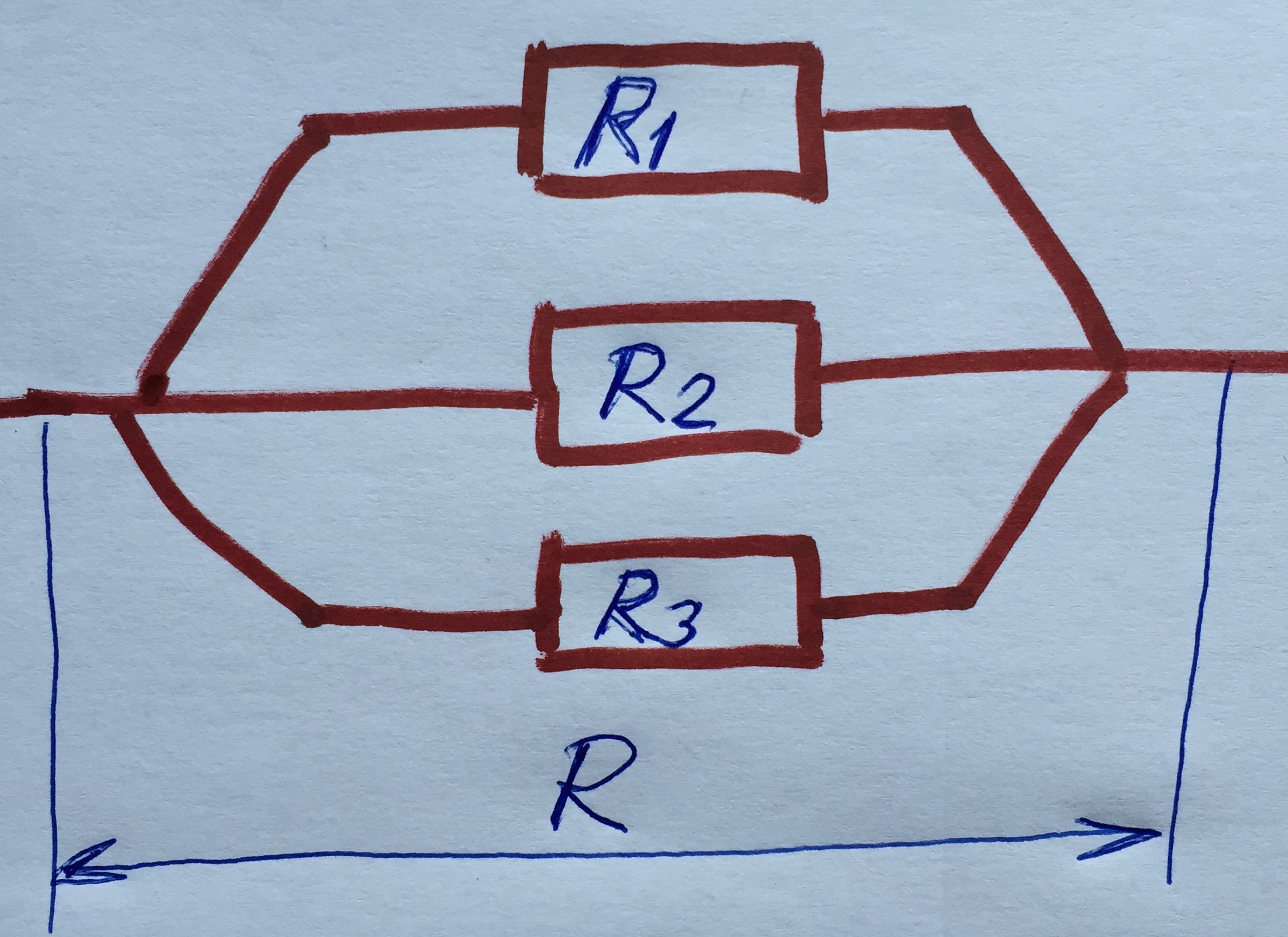
Övning 6 – parallellkopplade resistanser
Parallellkopplade komponenter är vanliga i elektroniska kretsar. Belysningspunkter i elnät i ett vanligt hus är parallellkopplade (en enkel julgransbelysning
är ofta seriekopplad).
För att beräkna den totala resistansen (R) över en krets måste den angivna formeln användas.
Övning 7 – obalans i en krets
Formeln är ett urklipp från makrot %SimUB. Formeln visar att om X = Y blir obalansen (UB) noll men om X och Y är olika blir det en viss obalans i kretsen.
Konstruktören har angivit att max 1% av alla kretsar får ha en obalans > 0.002. Vilket 'sigma' behövs för att tillfredsställa kravet? Pröva olika 'sigma', öka
eventuellt antal simulerade värden för att få entydigare bild. Kör också Minitab-makrot %SimUNB.
••••
Länkar
Confidence interval for p (ENG)
The animation shows how a confience interval for p should be intepreted. Here p
('proportion', 'fault rate', etc) is the unknown parameter to be estimated
from a dataset.
Several distributions with common μ and σ (ENG)
The animation shows several distributions with common μ and σ. By two slides these values can be changed
and the corresponding functions visualised.
Simulering av kapabilitetsindex Cpk
Ett kapabilitetsindex är ett index som försöker sammanfatta förhållandet mellan utfallet
från en process och dess specifikationer.
A mixture of distributions (ENG)
An animation that shows what happens when distributions are mixed.
Simulating a comparison of two proportions (ENG)
A simulation that shows some of the difficulties when comparing two proportions.
Animering av en enkel OC-kurva
Här animeras en enkel OC-kurva som beskriver vissa egenskaper hos ett enkel stickprovsförfarande.
Simulering av talet pi — Buffons nål
Här simuleras och animeras Buffons nål — ett klassiskt sätt att simulera det berömda talet pi.
Konfidensintervall
Här simuleras och animeras flera grundläggande egenskaper hos ett konfidensintervall.
Ett antal fördelningar
Initialt visas en Weibullfördelning men ett antal kontinuerliga och diskreta fördelningar kan visas via en länk. För varje fördelning kan parametrarna ändras
steglöst så att fördelningarnas form och läge uppdateras.
Avverkning av felrapporter
Simuleringen visar hur antal felrapporter minskar då antal 'ut' överstiger antal 'ut' och minskningen sker ungefär som en rät linje.
Variationen vid RTL ("Ready To Launch") påverkas kraftigt då 'utintensiteten' förändras.
Kvalitetsbristkostnader
Simulering av en enkel process (utan alternativa flöden) där en enhet kan ha upp till fem olika fel. Det finns tre teststationer där
felen kan upptäckas eller passera oupptäckta (den sista teststationen är kunden).
En Markovkedja
Simulering av en enkel s.k. Markovkedja. En sådan beskrivs ofta som en process med flera steg och där ett 'ärende' kan hoppa omkring med kanske
inget eller flera slut. En hiss kan ju gå från olika våningar men kommer aldrig fram medan ett bankärende eller felrapport kommer att avslutas förr eller
senare.
En Quincunx
En s.k. Quincunx är en enkel apparat där man låter kulor e.d. falla ned mot någon typ av stopp och på så sätt visa hur summan av
en mängd små händelser leder till ett normalfördelat utfall.
Minitab-makron
%2000 Makrot plottar 2000 punkter (som tidigare simulerats) och diagrammet visar en kanske oväntad form men helt i linje med statistisk teori. Kräver en viss kunskap om binomialfördelningen.%Birthday Makrot simulerar och illustrerar det klassiska födelsedagsproblemet "Hur stor grupp behövs för att hitta minst två personer med samma födelsedag?".
%CLT Makrot illustrerar den s.k. centrala gränsvärdessatsen (CLT). När ett antal värden summeras (t.ex. ett medelvärde) tenderar utfallet att bli mer normalfördelat då antal termer ökar. Se också %Die.
%CreDist Makrot skapar en teoretisk diskret sannolikhetsfördelning baserad på användarens indata. Dessutom simuleras data från denna fördelningen.
%Die En vanlig tärning används ofta för att illustrera statistisk teori. Här visas bl.a. hur fördelningen av en summa av värden snabbt närmar sig en normalfördelning. Se också %CLT.
%DistA Makrot ger teoretisk info och simulerar 12 olika sannolikhetsfördelningar som kan användas i praktiskt arbete. ('Cachy' är matematiskt extremt avvikande och bör studeras för just dessa egenskaper. Se t.ex. [3])
%DrawPin Makrot simulerar kastserier där varje resultat har två värden. Den observerade kvoten närmar sig det sanna värdet samtidigt som utfallet (summan) blir mer symmetriskt. Se också %CLT och %Die.
%DxDy Inom elektronitillverkning är det viktigt att anpassa olika masker mot varandra. Hur görs detta på bästa sätt om varje mask har måttoriktigheter? Makrot gör en matematisk optimering så att de kvarvarande felen blir så små som möjligt (dvs felens varians i X- och Y-led minimeras).
%Hdist Makrot simulerar det kortaste avståndet mellan två punkter i planet. Exemplet kommer från elektroniktillverkning där punkter för t.ex. komponenter och elektriska ledare skall sammanfalla utan alltför stora avvikelser. Se t.ex. [5], [6], [7].
%Hist Makrot gör en genomgång av och diskussion om begreppen histogram och sannolikhetsdiagram ('probability plot'). Användaren kan ändra parametervärden, antal, data, etc.
%LinC Linjärkombinationer uppstår då man sätter ihop detaljer, lägger ihop tider, beräknar medelvärden, etc, alltså då man adderar eller subtraherar mätvärden till en summa. Makrot illustrerar detta med en axeltapp som skall passa i en lagring. Se t.ex. [A good example...] och [Combination of...].
%Merror Mätfel är alltid ett aktuellt ämne då man studerar data. Vad är sannolikheten att ett uppmätt resultat, utanför givna specifikationer, verkligen är fel? Vad är sannolikheten att ett mätresultat, inom specifikationerna, verkligen är rätt? Naturligtvis kan man inte skilja mellan mätvärdet och det sanna värdet, man kan dock göra upprepade mätningar på t.ex. kända likare och sålunda få ett grepp om felet. Observera att även om mätvariabeln är kontinuerlig så blir ju resultatet av typ 'OK' respektive 'ej OK'.
%MinMax Ibland är man intresserad av extremvärden: 'hur stark är den svagaste länken i en kedja?' Värden som 'min', 'median', 'max' kallas på engelska för 'Order statistics'. Ett annat exempel: '5 % får understiga 15 mH' är en specifikation om 'order statistics' nämligen 5-percentilen. 'Order statistics' är något extra komplicerat men är värt att studera och känna till. Se t.ex. [Order statistics.doc] och [Fastest scorer.doc].
%Mix En mixture är en blandning av mätvärden och skall inte förväxlas med en kombination av variabler. En blandning av data är naturligtvis oerhört vanligt. Makrot ger teoretisk info och simulerar hur blandningar kan uppstå. Se t.ex. [57])
%OC 'OC' är en förkortning för 'Operating Characteristic' och används oftast inom stickprovsteori (som ju också är 'beslutsteori', dvs man fattar beslut om t.ex. partier av produkter och där det finns en risk att man fattar fel beslut p.gr.a resultatet i stickprovet.)
Makrot ritar tre olika grafer som är vanliga då man diskuterar OC-kurvor. Observera att makrot bara visar teoretiska resonemang, det finns inga simulerade data eller andra data. 'p' på X-axeln är processens felkvot, inte observerade data.
%PoAcc Makrot diskuterar Poissondata och ritar en graf med tre olika processer med olika parametervärden. (Dessa kan ändras inför en ny simulering, se detaljer i datafönstret.) I graferna ritas resultatet som ackumulerande, dvs för varje ny händelse så hoppar kurvan ett steg uppåt på Y-axeln. Detta kallas ibland för en 'pure birth process' dvs det finns inga 'deaths'. De tre färgade punkterna längst till höger anger förväntat resultat och graferna kommer att sluta som en slumpmässig variation runt dessa punkter i enlighet med Poisson-fördelningens egenskaper.
%PoisSim Makrot diskuterar en jämförelse mellan 'medelvärde' och 'median' i en Poissonfördelning. (Upprinnelsen är en IT-avdelning på ett större företag som ville börja redovisa 'median för antal störningar per månad' i stället för medelvärdet.) Det visar sig att medianen är långt mer okänslig mot förändringar i processen, detta ansågs vara bra ty det oroade inte kunderna! En utförlig diskussion: [27])
%Reg Regressionsanalys är en oerhört viktig analysform. Idén är att söka ett samband mellan ett mätresultat och en eller flera förklarande variabler. Grunderna presenteras i många böcker om statistisk analys och makrot understryker de viktigaste punkterna samt ger möjlighet att simulera samband för bättre förståelse.
%Rounding Den som använder 'normalitetstest' på data stöter ibland på 'Anderson-Darling'-test. Eftersom riktiga data oftast är begränsade till en, två eller tre decimaler, brukar testet förkasta hypotesen om 'normalitet'. Makrot simulerar data och diskuterar hur testet reagerar på olika avrundningar av data. Se också [79])
%ScrapCost Antag att vi producerar elektronikkomponenter, t.ex. mönsterkort. Vi börjar då med ett råmaterial, ett ämne, som vi sedan förädlar genom att borra hål för komponenter, etsa fram mönster, skyddslacka ytan, konturbearbeta. Varje sådan operation är inte helt felfri så i slutändan har man antagligen färre produkter än antal ämnen vid start.
Om vi har färre produkter än vi har lovat kunden uppstår kostnader av typ omstartskostnader, förseningskostnader, etc. Om vi i stället har fler produkter tvingas vi kassera eller ge bort dem utan ersättning. Hur skall man eller kan man resonera om det 'överantal' som man bör starta med? Makrot beräknar förväntad kostnad. Se också dokument i 'Statistikhörnan'.
%SimQ Många praktiska situationer kan beskrivas som köer – personer till betjäningsställen, ansökningar om bygglov, felrapporter i IT-utveckling, testning och omtestning av produkter i en produktionslina etc. Makrot simulerar en sådan enkel kö och ritar ett antal grafer. Köteori bygger ofta på s.k. Markovkedjor eller Markovprocesser och dessa är rikt dokumenterade på nätet och i litteraturen och väl värda uppmärksamhet.
%SimUB Praktiska situationer blir ibland extra komplicerade och då kan simulering vara ett sätt att få bra svar. Makrot beskriver ett fall där en elektrisk krets består av två resistanser. En matematisk formel används för att beräkna obalansen (UB) i kretsen. I praktiken finns det en viss variation mellan komponenterna innan de löds ihop till en krets och en central fråga är hur denna variation påverkar slutresultatet.
Makrot simulerar data med olika standardavvikelse på resistansen och redovisar sedan vilken andel kretsar som har ett UB-värde som ligger utanför specifikation. Ju mindre variation hos komponenterna desto bättre (och dyrare!) krets.
%Taxi Makrot diskurerar hur man kan skatta det högsta talet (N) i en serie typ 1, 2, 3, ...N och där man har ett stickprov från serien. Makrot redovisar två skattningsmetoder med förbluffande olika precision.
%Timing Makrot är populärt ty det simulerar mer och mer data i ett antal kolumner och mäter tiden och ger sålunde info om prestanda hos datorn (brukar ge upphov till jämförelser och diskussioner). Resultatet presenteras som en regressionsanalys (se %Reg) med två förklarande variabler.
%TwoNo Makrot simulerar en relativt enkel situation med två mått på samma enhet men där det är viktigt att rätt formulera frågan som skall besvaras. Se t.ex. [2])
%W Makrot ritar och simulerar fyra olika Weibullfördelningar givet parametervärden som anges i datafönstret.
%XbarS Makrot sammanfattar ett antal punkter om medelvärde och standardavvikelse samt simulerar värden som presenteras i några grafer. Datafönstret innehåller ett antal övningar.
Några dokument
Några erfarenheter
Några erfarenheter med att arbeta med data.
Ett antal dokument
Mer än 25 olika dokument om varierande område inom statistik och statistisk analys. Se t.ex. "What is sigma?" som har en
noggrann genom av vad sigma är, hur sigma skall tolkas, hur sigma kan beräknas, etc.
••••