Medelv.:

Stand.:

Min:

Max:

Medelvärde ('my'):

Standardavvikelse ('sigma'):

Stickprovsstorlek (2 – 99):

Antal stickprov (2 – 100):

Konfidensnivå (0.50 – 0.99):

%ConfInt (fig 1)...

%ConfInt (fig 2)...

%Nhist...

%Nhist (fig 1)...

%Nhist (fig 2)...

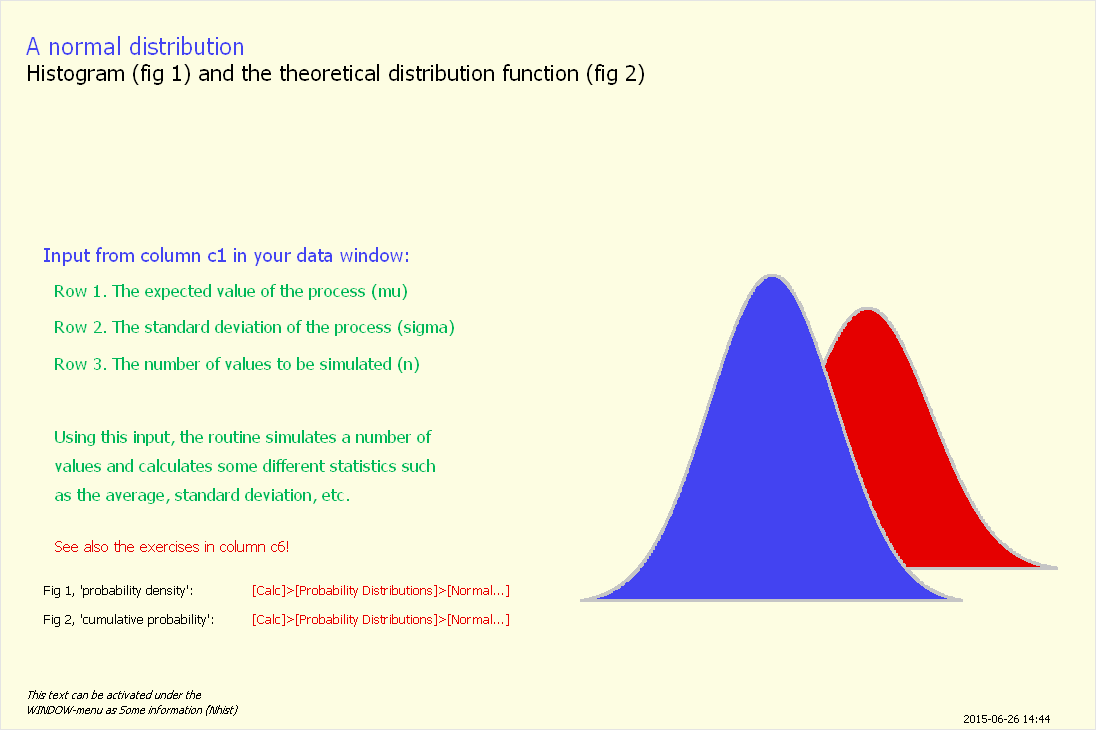
Rutan visar två fördelningar:

• den blå är är processen
• den röda fördelningen av medelvärden

Bägge fördelningarna har – som förväntat – samma teoretiska medelvärde. Fördelningen för medelvärden har – också förväntat – en mindre spridning, se formel under 'info'-knapp i den röda rutan. (Eftersom ytan under de bägge kurvorna är 1, måste den röda fördelningen bli högre än den blå i diagrammet.)

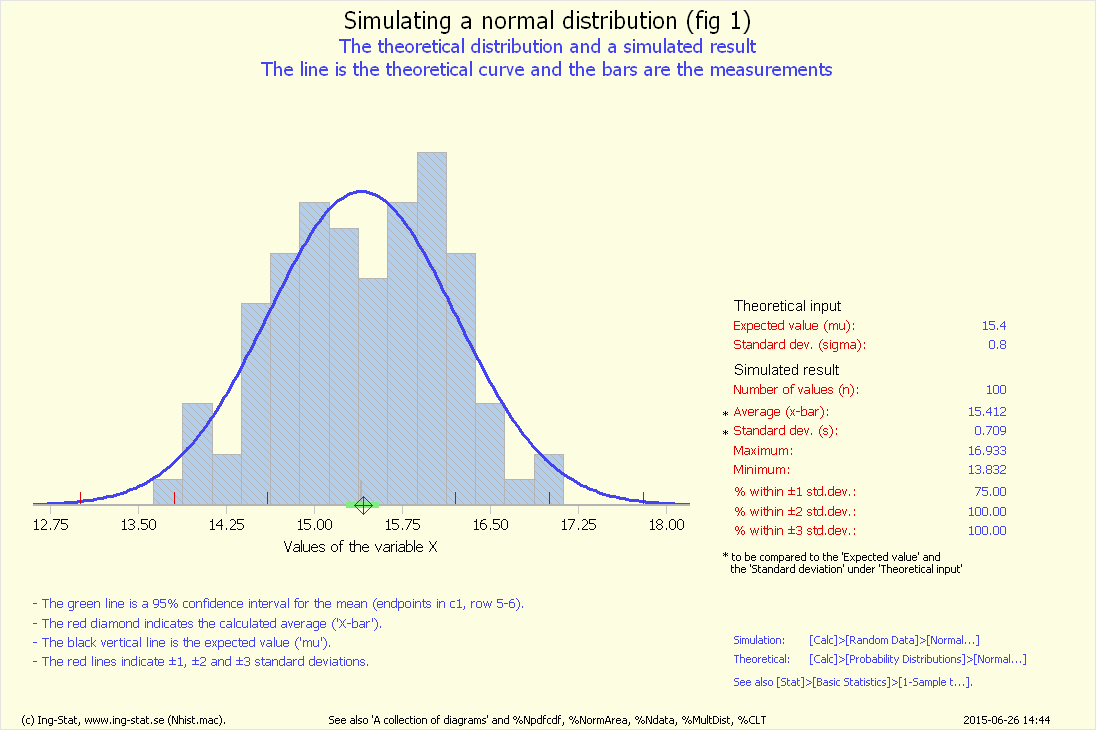
De blå punkterna är simulerade värden med processens medelvärde ('my') och standardavvikelse ('sigma'). Antal blå punkter är 'Stickprovsstorlek' * 'Antal stickprov'. Varje röd punkt är medelvärdet av data i ett enskilt stickprov. Antal röda punkter är alltså 'Antal stickprov'.

••••

'Kopiera/Klistra in' raden i rutan nedan till 'Session window' i Minitab vid "MTB >"-prompten och tryck sedan på [Enter]-knappen på tangentbordet.

Kommandot startar ett Minitab-makro (%ConfIntWeb) med parametrar enligt indata till vänster. Med dessa uppgifter simuleras ett antal konfidensintervall. (De två sista siffrorna anger vilka grafer som skall skrivas ut av Minitab.)

Om värdet ändras i någon av indatarutorna ändras också motsvarande kommando i rutan.

••••

Siffrorna visar processens parametrar:

• det teoretiska medelvärdet

• den teoretiska standardavvikelsen (sigma)

• den teoretiska standardavvikelsen för medelvärdet

Uttrycket för standardavvikelsen för medelvärdet:

Det är altså tydligt att när n ökas så minskar medelvärdets standardavvikelse. Detta verkar naturligt eftersom mer data borde ge en bättre skattning av μ.

Den röda fördelningen visar medelvärdets variation. Om n ("Stickprovsstorlek...") ökas så blir den röda fördelningen smalare.

••••

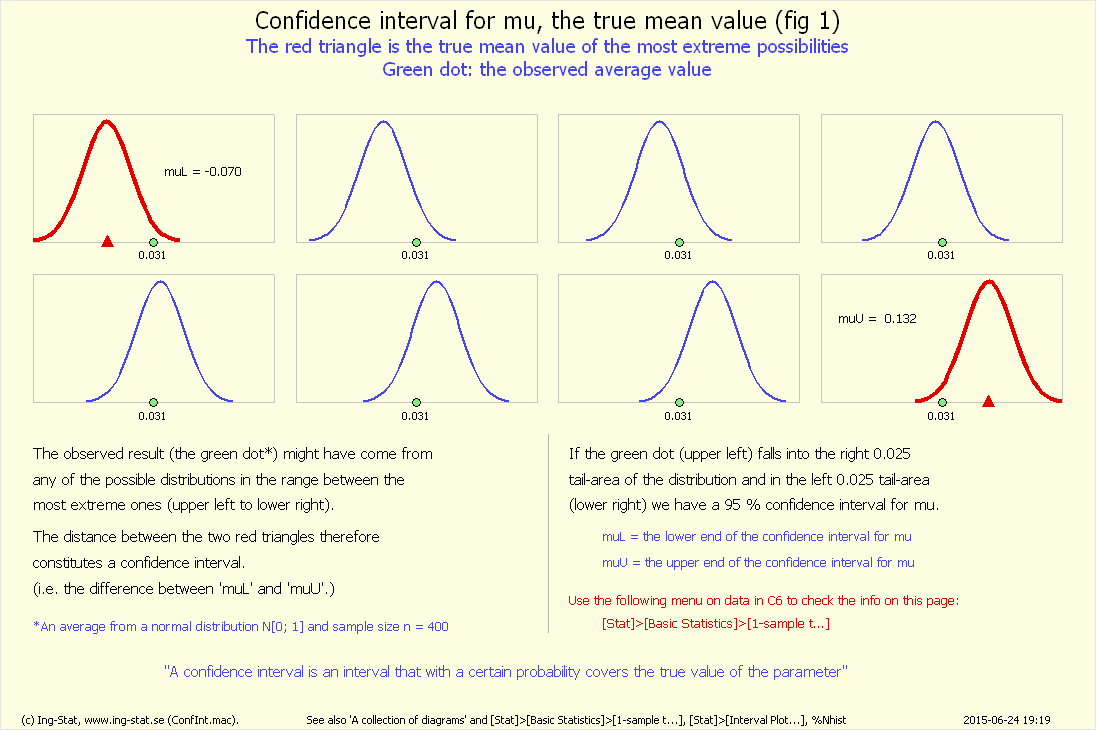
Allmänt.   Denna övning handlar om konfidensintervall för μ och dess tolkning. Dylika intervall är vanliga inom statistisk analys och handlar om att 'fånga in' det sanna värdet på en okänd parameter, här μ-värdet.

Beräkning av intervallet.   Många statistikprogram beräknar rutinmässigt intervallets ändpunkter och den formel som används här finns i PDF-dokumenten.

Tolkning av intervallet.   även om ett intervall för μ anges enkelt som t.ex. '4.5−7.6' skall det tolkas som att 'intervallet av μ-värden 4.5−7.6 inte kan förkastas som möjliga värden på μ'.

Mer info.   Nedanstående länkar ger mer information om denna och liknande situationer (obs att den andra länken handlar om 'felkvots'-parametern):

http://www.ing-stat.se/anim/konfint/konfint5.html

http://www.ing-stat.se/anim/konfbin/confbin3.php

••••

Förberedelser
Det finns fem olika 'info'-knappar. Klicka på alla och läs instruktioner och kommentarer. Formeln för att beräkna ett konfidensintervall finns i de två PDF-dokumenten "%ConfInt" och "Konfidensintervall". Klicka upprepade gånger på knappen [Repetera] och notera hur medelvärdena fördelas på talaxeln.

Övning 1 – olika n
Varje gång man beräknar ett medelvärde har man ett värde på 'medelvärdesvariabeln'. Ändra "Stickprovsstorlek" (n) till litet värde t.ex. 10 och tryck upprepade gånger på [Repetera]-knappen. Notera att den röda fördelning fick större standardavvikelse (blev 'bredare'). Öka n till t.ex. 90 och då blir den röda fördelningen smalare (till ett högre pris, nämligen ökat antal mätningar).

Övning 2 – olika antal stickprov
Sätt "Antal stickprov..." till ett högt värde, t.ex. 90. Notera att '+'-tecknen då fyller ut en stor del av den röda fördelningen. Om antal "Stickprov..." sätts till litet, t.ex. 4 ligger '+'-tecknen närmare medelvärdet. OBS att i en verklig situation har man ju bara ett stickprov och sålunda bara ett medelvärde.

Övning 3 – litet stickprov (n)
Konfidensintervallets längd bestäms av bl.a. den beräknade standardavvikelsen i stickprovet, se formeln i PDF-dokumenten. Men om stickprovet (n) är litet, kommer denna beräkning att ha stor variation och sålunda även intervallets längd. OBS att konfidensintervallets egenskaper, att det innefattar det sanna värdet på den okända parametern, kvarstår. (Statistikt okunniga personer avfärdar ibland resultatet med '...för litet stickprov...'. 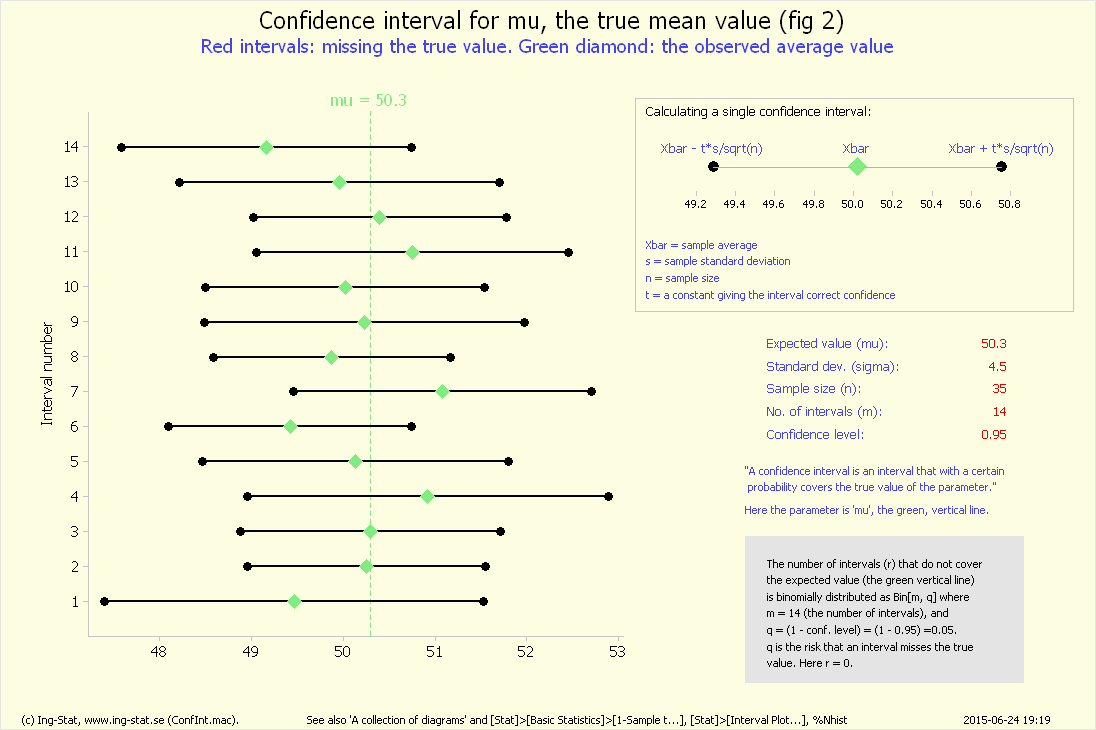Det kan vara sant att intervallets längd är stort men dess grundläggande egenskap kvarstår.) Diagrammet '%ConfInt fig 2' visar stor variation mellan intervallens längd.
(Se också http://www.ing-stat.se/anim/konfint/konfint5.html)

Övning 4 – stort stickprov (n)
När n är stort kommer intervallens längd att minska och variationen mellan dem bli mindre. Detta sker ju till ett visst pris, nämligen fler mätningar. (Om man vill halvera längden på ett konfidensintervall behöver man i princip fyra gånger större stickprov. Detta beror på att minskningen beror på 'roten ur n', se formeln i PDF-dokumenten.)
Diagrammet '%ConfInt fig 2' visar mindre variation mellan intervallens längd.
(Se också http://www.ing-stat.se/anim/konfint/konfint5.html)

Övning 5 – låg konfidensnivå
Konfidensnivån, som anger sannolikheten att intervallet omfattar den okända parameterns sanna värde, är väldigt viktig och central. En konfidensnivå på t.ex. 0.50 betyder att vartannat konfidensintervall förväntas missa parametern. Om en forskare skulle använda denna nivå i sina redovisningar skulle naturligtvis ingen tro på något rapporterna. (Fördelen är, ur forskarens synpunkt, att intervallen blir korta och till synes imponerande). Diagrammet '%ConfInt fig 2' visar att ungefär 50 av de beräknade intervallen missar rätt parametervärde.

Övning 6 – hög konfidensnivå
Om konfidensnivån är hög kommer praktiskt taget alla intervall att innefatta det sanna värdet på parametern. Det betyder också att intervallen blir längre och man kan fundera på om det är nödvändigt med en 'väldigt hög konfidensnivå'. Diagrammet '%ConfInt fig 2' visar att praktiskt taget inget intervall missar rätt parametervärde.

••••