Info, referenser, m.m...

![]()
![]()
![]()
![]()
![]()
Analys av p – en proportion
Denna sida innehåller övningar och kommentarer vid beräkning av en proportion ('procentsats').
Varje punkt är en komponent, människa, träd... (se 'info'-knappen)
Sann felkvot (p):
Antal enheter i populationen (N):
Antal felaktiga enheter (X):
Felkvot i simuleringen (X/N):
Antal enheter i stickprov (n):
Antal felaktiga i stickprov (x):
Observerad felkvot (p-hat = x/n):
Visa 'fig 1' i Minitab
Visa 'fig 2' i Minitab
%Confp (fig 1)...
%Confp (fig 2)...
![]()
Rutorna innehåller parametervärden som används för att simulera data. En ändring registreras direkt i kommandorutan till höger:
Sann felkvot (p): I dessa övningar simuleras enheter som är antingen 'OK'/'ej OK' eller 'frisk'/'sjuk', etc. Sannolikheten för 'ej OK' är 'p' (och sålunda är sannolikheten 1-p för 'OK'). 'p' är den okända men intressanta parametern.
Antal enheter i populationen (N): Anger antal prickar i diagrammet. (Populationens storlek är nästan alltid – märkligt nog – betydelselös i stickprovssammanhang.)
Antal felaktiga enhetet (X): Antal (simulerat) röda ringar i diagrammet.
Felkvot i simuleringen (X/N): Beräknad felkvot (bör bli nära 'Sann felkvot').
Antal enheter i stickprov (n): Är det antal enheter som 'avsynats'.
Antal felaktiga i stickprovet (x): Är antalet felaktiga som hittats i stickprovet.
Observerad felkvot (p-hat = x/n): Felkvoten i stickprovet (bör bli nära 'Sann felkvot').
"Visa 'fig 1'...": Minitab-makrot skapar två olika grafer och det är inte alltid önskvärt att dessa skapas vid varje övning. Det är sålunda möjligt att förhindra att en eller flera grafer skapas. (Exempel på grafer finns under länkarna "%Confp (fig 1)...".)
Observera att ordet 'felkvot' kan lika gärna vara 'rättkvot' eller 'andel som överlevde 5 år' eller någon annan proportion som studeras.
Alla förändringar som görs i indatarutorna registreras på sidans 'kommandoruta'. För att göra analys i Minitab måste raden '%ConfpWeb...' manuellt kopieras in i Minitab och aktiveras. Därefter kan analysen utföras.
Det finns fyra knappar som visar övningar och texter (övningar i pdf-format kan skrivas ut och användas).
De två blå länkarna visar
exempel på grafer som skapas av %Confp-makrot i Minitab.
••••
• Varje grå punkt motsvarar en komponent eller en människa eller ett träd eller ett djur eller något annat och där varje enhet tillhör en av två grupper ('OK'/'ej OK', 'frisk/sjuk' osv.).
• Varje röd ring är en felaktig komponent eller en sjuk människa, etc.
• Varje kryss är en enhet som ingår i stickprovet och som kontrolleras eller undersöks.
Klicka på 'Repetera'-knappen för att repetera simuleringen.
(Det finns inga felbedömningar, dvs en komponent som klassats som felaktig är verkligen felaktig):
'Visa/dölj population' (alla grå punkter)
'Visa/dölj alla felaktiga' (alla röda ringar)
'Visa/dölj stickprov' (alla kryss)
••••
'Kopiera/Klistra in' raden i rutan nedan till 'Session window' i Minitab vid "MTB >"-prompten och tryck sedan på [Enter]-knappen på tangentbordet.
Kommandot startar ett Minitab-makro (%ConfpWeb) där första siffran är stickprovets storlek och den andra siffran
är antal felaktiga i stickprovet. (Obs att populationens storlek inte ingår i analysen.)
Med dessa uppgifter beräknas inte
bara felkvoten utan också ett konfidensintervall för 'p'.
(De två övriga siffrorna anger vilka grafer som skall skrivas ut av Minitab.)
Om värdet ändras i någon av indatarutorna ändras också motsvarande kommando i rutan.
••••
Allmänt. Denna övning handlar om analys av en proportion ('procentsats') inklusive ett s.k. konfidensintervall och dess tolkning. Dylika intervall är vanliga inom statistisk analys och handlar om att 'fånga in' det sanna värdet på en okänd parameter, här p-värdet.
Beräkning av intervallet. Många statistikprogram beräknar rutinmässigt intervallets ändpunkter. Förvånande nog är detta ganska komplicerat för ett p-värde (speciellt som en procentsats anses vara ganska enkel). Denna beräkning redovisas inte här.
Tolkning av intervallet. Även om ett intervall anges enkelt som t.ex. '0.045 - 0.135' (dvs 'intervallet för p är 4.5 till 13.5%') skall det tolkas som att 'intervallet av p-värden 0.045-0.135 inte kan förkastas som möjliga värden på p'.
Formler.
Sannolikheten för ett visst utfall (ett visst antal felaktiga i stickprovet) beror på situationen. Om man drar ett stickprov (n)
ur en tydlig och avgränsad population (N) används en s.k. hypergeometrisk sannolikhetsfördelning.
Om man i stället
dragit stickprovet utan en definerad och avgränsad population (kanske en oändligt stor population) används en
s.k. binomialfördelning.
Nedanstående formler redovisar teoretiskt medelvärde ('my') och standardavvikelsen ('sigma') för proportionen. För bägge
modellerna (hypergeometrisk och binomial) gäller samma teoretiskt medelvärde (p). Det är som man kan förvänta – om
det sanna värdet på proportionen är 0.14 så förväntar man samma resultat i stickprovet. Den övre formeln för standardavvikelsen
gäller binomialfördelningen och de två formlerna är desamma förutom faktorn (N-n)/(N-1). Denna ger en mindre standardavvikelse
för p då man tar stickprov ur en begränsad population. Emellertid blir faktorn lätt nära ett och sålunda utan större betydelse:
Mer info.
Nedanstående länkar ger mer information om denna och liknande situationer:
http://www.ing-stat.se/anim/konfbin/confbin3.php
http://www.indstat.se/simuleringar/simuleringar.php
••••
Förberedelser
Det finns fem olika 'info'-knappar. Klicka på alla och läs instruktioner och kommentarer. Klicka upprepade gånger på 'Repetera'-knappen och se hur
grafen förändras och att resultaten skrivs i respektive fält.
Övning 1 – stort N
Stickprovets storlek i förhållande till populationen har i de allra flesta fall väldigt liten betydelse. Öka successivt N och se att
proportionens sigma (röda siffror rad 2 och 3) förändras. Då sidan laddas är värdena 0.032 respektive 0.023. Då N ökas ökar också
den undre siffran och närmar sig och blir till slut samma som det övre sigma-värdet.
Det betyder att trots att stickprovets andel av populationen minskar, så ökar inte osäkerheten.
Övning 2 – n = N
Sätt både n och N till, säg, 500. Det betyder att hela populationen avsynas och därmed är osäkerheten noll, det undre sigma = 0.
Klicka på den övre 'info'-knappen och titta på den undre sigmaformeln. Då n = N blir faktorn (N - n)/(N - 1) noll
och sålunda hela uttrycket 0.
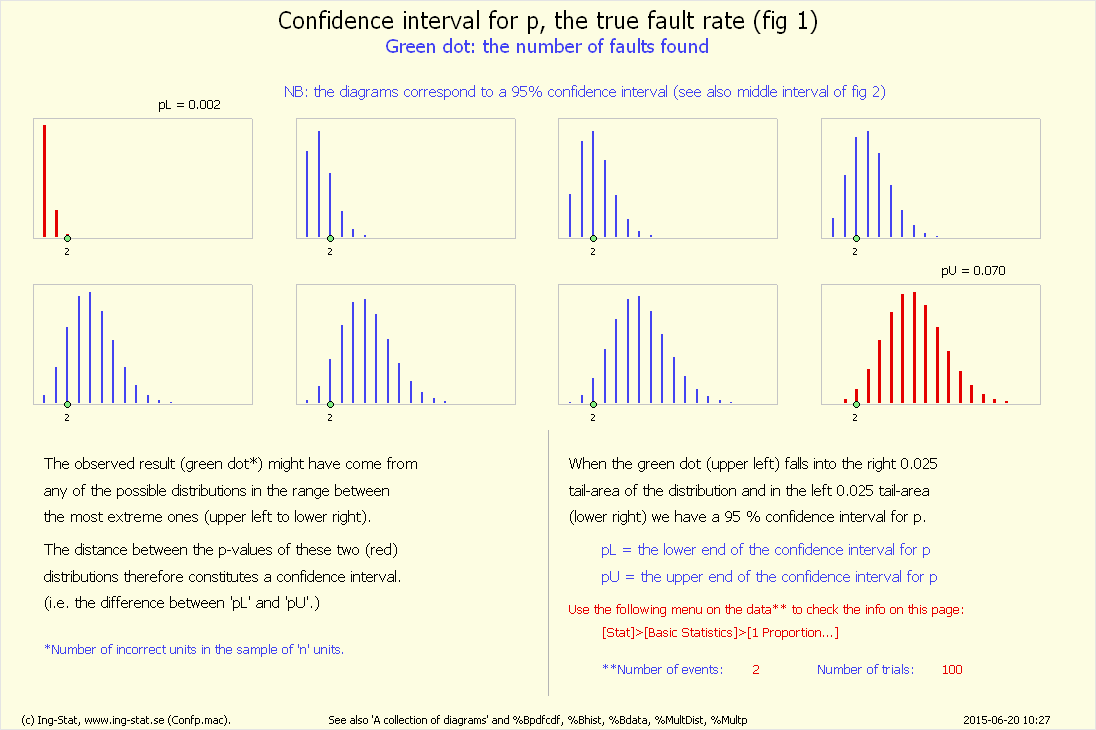
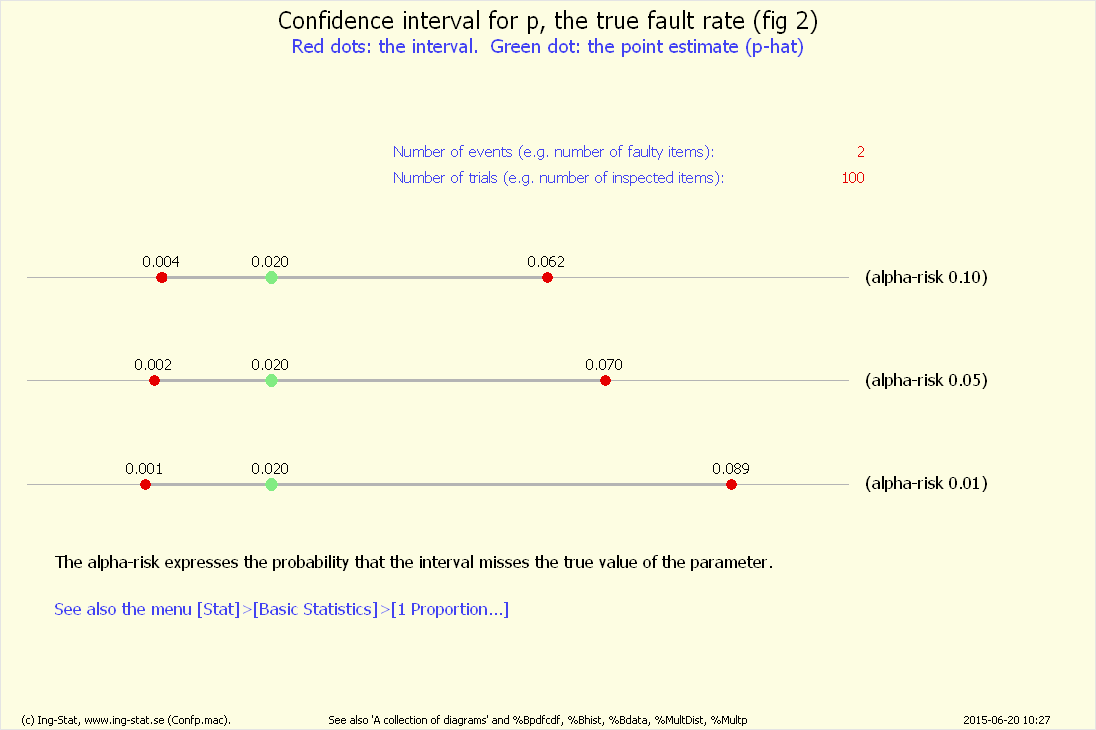
Övning 3 – beräkning av ett konfidensintervall
Ett konfidensintervall är ett intervall som med en viss sannolikhet omfattar det sanna värdet för parametern ifråga, här p-värdet.
Själva beräkningen är komplicerad och kräver ett statistikprogram. Den senaste simuleringen finns i kommandorutan och skall kopieras över till Minitab.
Då genereras två grafer med dels illustration av begreppet konfidensintervall, dels tre olika intervall (tre olika säkerheter).
(Se också http://www.ing-stat.se/anim/konfbin/confbin3.php)
Övning 4 – 0 felaktiga i stickprovet
Antag att man fått 0 felaktiga i stickprovet. Detta betyder knappast att den sanna felkvoten är 0, kanske bara låg. Det är dock möjligt att beräkna
ett konfidensintervall. Gör en Minitab-körning med de givna uppgifterna ("0 fel" är förprogrammerat). Notera att konfidensintervallet blir ganska skevt.
(Se också dokumentet A fairy tale på sidan http://www.ing-stat.se/art1.php.)
Övning 5 – simulering som illustrerar övning 4
Om övning 4 körs med stickprovsstorlek 150 blir den övre gränsen för ett 95%-igt konfidensintervall 0.0198 (dvs nästan 2 procent). Det skall tolkas som
att det finns en risk (5%) att få 0 felaktiga i stickprovet trots att felkvoten är så hög som 0.02.
Se utfallet från histogram och 'Tally'-kommandot i Minitab.
••••
De tre sifferuppgifterna visar det teoretiska medelvärdet och den teoretiska standardavvikelsen (sigma) för proportionen (två värden).
Det första sigma gäller om stickprovet kan anses komma från en oänligt stor population ('binomialfördelning').
Det andra sigma
gäller om stickprovet är draget ur en definierad och begränsad population (N) ('hypergeometrisk fördelning').
Det första värdet är alltid större eller lika med det undre värdet.
Ändra (N) till allt större värden och se att de två sigma blir mer och mer lika. Detta visar att populationens storlek förlorar i betydelse, det viktigaste är stickprovets storlek.
••••